容斥原理是一种计数的好方法。容指的是包容包括,斥指的是排斥。其实也就是在解决重叠问题。需要用到很重要的工具图-韦恩图。
1.两个组的问题(二量容斥)
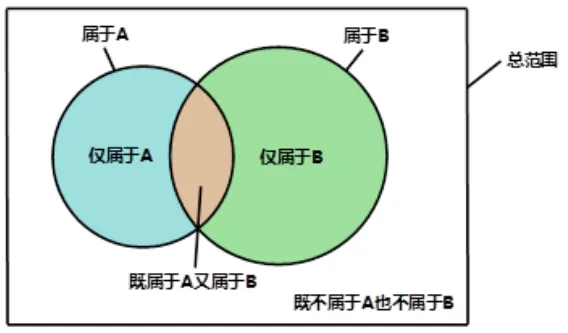
2.三个组的问题(三量容斥)
把n+1个苹果放进n个抽屉,至少有一个抽屉有2个苹果。苹果数 ÷ 抽屉数 = 商...余数
(至少有一个抽屉有(商+1)个苹果)
1.基础应用:
求抽屉最多、苹果总数最少、苹果数最多的抽屉最少多少
2.进阶应用
染色问题
如:4行n列方格,每列染2个白色,求n至少多少能保证至少6列染色相同。
分析:
得分问题
题目:10道题,答对5分,答对一半3分,答错0分,至少多少人能保证3人得分相同。
分析:
小雨总结
容斥原理核心
两个集合:A+B-A∩B
三个集合:A+B+C-A∩B-A∩C-B∩C+A∩B∩C
包含"都没有":记得加上"都不"的人数
抽屉原理核心
基本公式:至少数 = 商 + 1
解题步骤:
确定什么是"苹果"(要分配的东西)
确定什么是"抽屉"(分配的对象或状态)
计算抽屉数量
用总数÷抽屉数,得到商和余数
结论:至少有一个抽屉有(商+1)个苹果
实用技巧
画韦恩图:帮助理解容斥原理
最不利原则:抽屉原理中考虑最坏情况
从反面思考:有时求"至少"可以从"最多不"的角度考虑
注意包含关系:容斥原理中要理清各部分的包含关系
通过系统学习这两个原理,能够解决很多生活中的实际问题,如统计人数、安排物品、保证某种情况一定发生等,是很重要的数学思维工具。