n
9.2.3 总体集中趋势的估计
［学习目标］ 1.能够正确计算平均数、中位数、众数.(重点)2.掌握利用样本的平均数、众数、中位数估计总体的集中趋势的方法，从而解决相关的实际问题.3.理解用样本的数字特征、频率分布直方图估计总体的集中趋势.(难点)
导语
在初中的学习中我们已经了解到，平均数、中位数和众数等都是刻画“中心位置”的量，它们从不同角度刻画了一组数据的集中趋势，下面我们通过具体实例进一步了解这些量的意义，探究它们之间的联系与区别，并根据样本的集中趋势估计总体的集中趋势.
一、众数、中位数、平均数
问题1如何求一组数据的众数、中位数和平均数？
提示 平均数：用所有数据相加的总和除以数据的个数，需要计算才可求出.
中位数：将数据按照从小到大或从大到小的顺序排列，如果数据的个数是奇数，则处于最中间位置的数就是这组数据的中位数；如果数据的个数是偶数，则最中间两个数据的平均数是这组数据的中位数.它的求出不需或只需简单的计算.
众数：一组数据中出现次数最多的那个数，不必计算就可求出.
知识梳理
1.众数：一组数据中出现次数最多的数.
2.中位数：把一组数据按从小到大(或从大到小)的顺序排列后，当数据个数是奇数时，处在最中间的数是中位数；当数据个数是偶数时，最中间两个数的平均数是中位数.
3.平均数：如果有n个数x1，x2，…，xn，
那么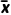
=
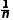(x1+x2+…+xn)叫做这n个数的平均数.
例1 在一次中学生田径运动会上，参加男子跳高的17名运动员的成绩如表所示.
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
分别求出这些运动员成绩的众数、中位数与平均数.
解在这17个数据中，1.75出现了4次，出现的次数最多，即这组数据的众数是1.75.表中的17个数据可看成是按从小到大的顺序排列的，其中第9个数据1.70是最中间的一个数据，即这组数据的中位数是1.70.这组数据的平均数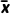
=
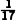×(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80×1+1.85×1+1.90×1)=
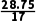≈1.69.
故17名运动员成绩的众数、中位数、平均数依次为1.75m，1.70m，1.69m.
反思感悟平均数、众数、中位数的计算方法
平均数一般是根据公式来计算的；计算中位数时，可先将这组数据按从小到大或从大到小的顺序排列，再根据相关数据的个数是奇数还是偶数而定；众数是看出现次数最多的数.
跟踪训练1 已知一组数据为52，49，48，54，47，48，55，52，则该组数据的中位数为，众数为，平均数为.
答案 50.5 48和52 50.625
解析把这组数据从小到大排列为47，48，48，49，52，52，54，55.中位数为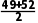
=50.5，众数为48和52，平均数为
=
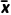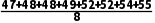=50.625.
二、总体集中趋势的估计
问题2我们知道平均数和中位数都描述了数据的集中趋势，它们的大小关系和数据分布的形态有关.从下面的三幅图中，你能得到平均数和中位数的大小存在什么关系吗？
提示 一般来说，对一个单峰的频率分布直方图来说，如果直方图的形状是对称的(图(1))，那么平均数和中位数应该大体上差不多；如果直方图在右边“拖尾”(图(2))，那么平均数大于中位数；如果直方图在左边“拖尾”(图(3))，那么平均数小于中位数.也就是说，和中位数相比，平均数总是在“长尾巴”那边.
问题3什么样的问题可以用平均数描述？什么样的问题可以用中位数描述？什么样的问题可以用众数描述？
提示 一般地，对数值型的数据(如用水量、身高、收入、产量等)集中趋势的描述，可以用平均数、中位数；而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述，可以用众数.
例2某校举行演讲比赛，10位评委对两位选手的评分如下：
甲 7.5 7.5 7.8 7.8 8.0 8.0 8.2 8.3 8.4 9.9
乙 7.5 7.8 7.8 7.8 8.0 8.0 8.3 8.3 8.5 8.5
选手的最终得分为去掉一个最低分和一个最高分之后，剩下8个评分的平均数，那么，这两位选手的最后得分是多少？若直接用10位评委评分的平均数作为选手的得分，两位选手的排名有变化吗？你认为哪种评分办法更好？为什么？
解甲选手的最后得分为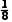
×(7.5+7.8+7.8+8.0+8.0+8.2+8.3+8.4)=8，
乙选手的最后得分为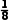
×(7.8+7.8+7.8+8.0+8.0+8.3+8.3+8.5)=8.0625.
若直接用10位评委评分的平均数作为选手的得分，
则甲选手的得分为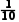
×(7.5+7.5+7.8+7.8+8.0+8.0+8.2+8.3+8.4+9.9)=8.14，
乙选手的得分为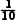
×(7.5+7.8+7.8+7.8+8.0+8.0+8.3+8.3+8.5+8.5)=8.05.
去掉最高分与最低分时，甲的得分小于乙的得分，即乙的排名靠前；若直接用10位评委评分的平均数作为得分，则甲的得分大于乙的得分，即甲的排名靠前.两种评分下，甲、乙两位选手的排名不同，去掉一个最低分和一个最高分之后，剩下8个评分的平均数作为选手的最后得分更好，这是因为平均数对样本数据的极端值比较“敏感”.
反思感悟众数、中位数、平均数的意义
(1)样本的众数、中位数和平均数常用来表示样本数据的“中心值”，其中众数和中位数容易计算，不受少数几个极端值的影响，但只能表达样本数据中的少量信息，平均数代表了数据更多的信息，但受样本中每个数据的影响，越极端的数据对平均数的影响也越大.
(2)当一组数据中有不少数据重复出现时，其众数往往更能反映问题，当一组数据中个别数据较大时，可用中位数描述其集中趋势.
跟踪训练2 某高校甲、乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1，2，3，4，5，共五个等级)的条形图如图所示，则甲成绩等级的中位数与乙成绩等级的众数分别是( )
A.3，5B.3，3
C.3.5，5D.3.5，4
答案 C
解析由条形图可得，甲同学共有10门选修课，将这10门选修课的成绩等级从低到高排序后，第5，6门的成绩等级分别为3，4，故中位数为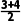
=3.5，乙成绩等级的众数为5.
三、利用频率分布直方图估计总体的集中趋势
例3某校从参加高一年级期末考试的学生中抽出60名，将其物理成绩(均为整数)分成六段［40，50)，［50，60)，…，［90，100］后画出如图所示的频率分布直方图.观察图中的信息，回答下列问题：
(1)估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数)；
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
解(1)众数是频率分布直方图中最高小矩形底边中点的横坐标，所以众数m=75.0.
前3个小矩形面积和为0.01×10+0.015×10+0.015×10=0.4<0.5，
前4个小矩形面积和为0.4+0.03×10=0.7>0.5，
所以中位数n=70+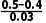
≈73.3.
(2)依题意得，60及60以上的分数在第三、四、五、六组，频率和为(0.015+0.03+0.025+0.005)×10=0.75，
所以估计这次考试的物理成绩的及格率是75%.
利用组中值估算抽样学生的平均分为45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
则估计这次考试物理成绩的平均分是71分.
反思感悟利用频率分布直方图求众数、中位数以及平均数的方法
(1)众数即为出现次数最多的数，所以它的频率最高，在最高的小矩形中.中位数即为从小到大中间的数(或中间两数的平均数).平均数为每个小矩形底边中点的横坐标与小矩形面积乘积之和.
(2)用频率分布直方图求得的众数、中位数不一定是样本中的具体数.
跟踪训练3 根据如图所示的频率分布直方图求出样本数据的众数、中位数和平均数.
解在［124.5，126.5)中的数据最多，取这个区间的中点值作为众数的近似值，得众数约为125.5.中位数左边和右边的直方图的面积相等，设中位数为x，则由图可知x在区间［124.5，126.5)内，则(x-124.5)×0.2+2×0.075+2×0.05=0.5，解得x=125.75，即中位数约为125.75.使用组中值求平均数，则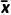
=121.5×0.1+123.5×0.15+125.5×0.4+127.5×0.2+129.5×0.15=125.8.即平均数约为125.8.
通过网盘分享的文件：同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享
