n
7.1.1 数系的扩充和复数的概念
[学习目标] 1.了解引进虚数单位i的必要性,了解数系的扩充过程.2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念.(重点)3.掌握复数代数形式的表示方法及分类,理解复数相等的充要条件.(难点)
导语
1545年,意大利数学家、物理学家卡尔丹在其所著《重要的艺术》一书中提出将10分成两部分,使其积为40的问题,即求方程x(10-x)=40的根,他求出的根为5+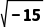 和5-
和5-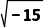 ,积为25-(-15)=40.由于这只是单纯从形式上推广而来,并且人们原先就已断言负数开平方是没有意义的.负数真的不能开平方吗?
,积为25-(-15)=40.由于这只是单纯从形式上推广而来,并且人们原先就已断言负数开平方是没有意义的.负数真的不能开平方吗?
一、复数的有关概念
问题我们知道,方程x2+1=0在实数集中无解,联系从自然数集到实数集的扩充过程,你能给出一种方法,适当扩充实数集,使这个方程有解吗?
提示 为了解决x2+1=0这样的方程在实数系中无解的问题,我们设想引入一个新数i,使得x=i是方程x2+1=0的解,即使得i2=-1.
知识梳理
1.复数
(1)定义:我们把形如a+bi(a,b∈R)的数叫做复数,其中i叫做虚数单位,满足i2=-1.
(2)表示方法:复数通常用字母z表示,即z=a+bi(a,b∈R),其中a叫做复数z的实部,b叫做复数z的虚部.
2.复数集
(1)定义:全体复数构成的集合C={a+bi|a,b∈R}叫做复数集.
(2)表示:通常用大写字母C表示.
注意点:
(1)i2=-1.
(2)i和实数之间能进行加法、乘法运算.
例1写出下列复数的实部、虚部:
1+3i,-2,-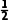 i,
i,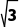 +
+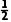 ,10+
,10+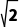 i,0,i2.
i,0,i2.
解
| 1+3i | -2 | -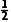 i i | 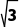 + +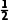
| 10+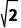 i i | 0 | i2 |
实部 | 1 | -2 | 0 | 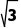 + +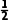
| 10 | 0 | -1 |
虚部 | 3 | 0 | -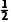 | 0 | 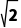
| 0 | 0 |
反思感悟复数的代数形式z=a+bi,只有当a,b∈R时,a才是z的实部,b才是z的虚部,且注意虚部不是bi,而是b.
跟踪训练1复数z=2i+3i2的实部是( )
A.0B.2C.3D.-3
答案 D
解析由于i2=-1,则z=2i+3i2=-3+2i,所以实部是-3.
二、复数的分类
知识梳理
1.复数z=a+bi(a,b∈R)可以分类如下:
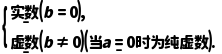
2.复数集、实数集、虚数集、纯虚数集之间的关系
例2已知m∈R,复数z=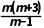 +(m2+2m-3)i,当m为何值时,
+(m2+2m-3)i,当m为何值时,
(1)z∈R;
(2)z是虚数;
(3)z是纯虚数.
解(1)若z∈R,则m需满足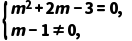
解得m=-3.
(2)若z是虚数,则m需满足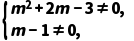
解得m≠1且m≠-3.
(3)若z是纯虚数,则m需满足
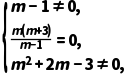 解得m=0.
解得m=0.
反思感悟(1)利用复数的分类求参数时,应将复数化为代数形式z=a+bi(a,b∈R).特别注意若z为纯虚数,则b≠0且a=0.
(2)要注意确定使实部、虚部有意义的条件,再结合实部与虚部的取值求解.
跟踪训练2(1)(多选)下列说法正确的是( )
A.对于复数a+bi(a,b∈R),若a=0,则a+bi为纯虚数
B.对于复数a+bi(a,b∈R),若b=0,则a+bi为实数
C.若a∈R,则(a2+1)i是纯虚数
D.实数集是复数集的真子集
答案 BCD
解析对于复数a+bi(a,b∈R),若a=0,b=0,则a+bi为实数0,若b=0,则a+bi=a为实数,故A错误,B正确;
若a∈R,则a2+1≠0,所以(a2+1)i是纯虚数,故C正确;显然D正确.
(2)已知m∈R,复数z=lg m+(m2-1)i,当m为何值时,
①z为实数;②z为虚数;③z为纯虚数.
解①当z为实数时,m需满足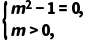
解得m=1.
②当z为虚数时,m需满足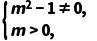
解得m>0且m≠1.
③当z为纯虚数时,m需满足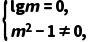 无解,
无解,
即不存在m使z为纯虚数.
三、复数相等的充要条件
知识梳理
在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),我们规定:a+bi与c+di相等当且仅当a=c且b=d.特殊地,a+bi=0⇔a=b=0.
例3(1)若(x+y)+yi=(x+1)i,求实数x,y的值.
解由复数相等的充要条件,得
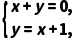 解得
解得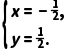
(2)已知复数x2-1+(y+1)i大于复数2x+3+(y2-1)i.求实数x,y的取值范围.
解由题意得,两个复数都是实数.
因为x2-1+(y+1)i>2x+3+(y2-1)i,
所以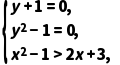
解得y=-1且x<1-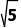 或x>1+
或x>1+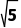 ,即实数x,y的取值范围为x<1-
,即实数x,y的取值范围为x<1-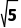 或x>1+
或x>1+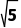 =-1.
=-1.
反思感悟复数相等问题的解题技巧
(1)必须是复数的代数形式才可以根据实部与实部相等,虚部与虚部相等列方程组求解.
(2)根据复数相等的条件,将复数问题转化为实数问题,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现.
(3)如果两个复数都是实数,可以比较大小,否则是不能比较大小的.
跟踪训练3复数z1=(2m+7)+(m2-2)i,z2=(m2-8)+(4m+3)i,m∈R,若z1=z2,则m=.
答案 5
解析因为m∈R,z1=z2,
所以(2m+7)+(m2-2)i=(m2-8)+(4m+3)i.
由复数相等的充要条件,得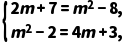
解得m=5.
1.知识清单:
(1)数系的扩充.
(2)复数的概念.
(3)复数的分类.
(4)复数相等的充要条件.
2.方法归纳:方程思想.
3.常见误区:未化成z=a+bi(a,b∈R)的形式.
1.在2+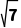 i,8+5i,(1-
i,8+5i,(1-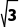 )i,0.618这几个数中,纯虚数的个数为( )
)i,0.618这几个数中,纯虚数的个数为( )
A.0B.1C.2D.3
答案 C
解析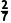 i,(1-
i,(1-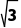 )i是纯虚数,2+
)i是纯虚数,2+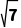 是实数,8+5i是虚数.故纯虚数的个数为2.
是实数,8+5i是虚数.故纯虚数的个数为2.
2.若复数z=ai2-bi(a,b∈R)是纯虚数,则一定有( )
A.b=0B.a=0且b≠0
C.a=0或b=0D.ab≠0
答案 B
解析z=ai2-bi=-a-bi,

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享