文氏图是展示三段论逻辑结构的常用工具,其绘制依据是大项(P)、小项(S)、中项(M)的外延关系;而三段论可以划分为四个格:主谓格、谓谓格、主主格、谓主格。,划分依据是中项在大前提和小前提中的位置,其中,前三种格为常见形式。第一格:主谓格:中项位置在大前提主项,小前提谓项,这是演绎推理的典型结构
推理模型:大前提 M→P;小前提 S→M;结论 S→P
大中小项的外延关系:
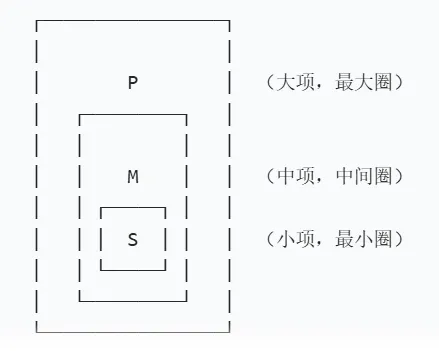
示例1:所有金属(M)都是导体(P),铁(S)是金属(M),结论:铁(S)是导体(P)
示例2:所有金属(M)不是绝缘体(P);有些合金(S)是金属(M);所以,有些合金(S)不是绝缘体(P)。
第二格:谓谓格:中项位置在大小前提中的谓项,推理结论必为否定判断。
推理模型:所有 P 都属于 M,所有 S 都不属于 M → 所有 S 都不属于 P
大中小项的外廷关系
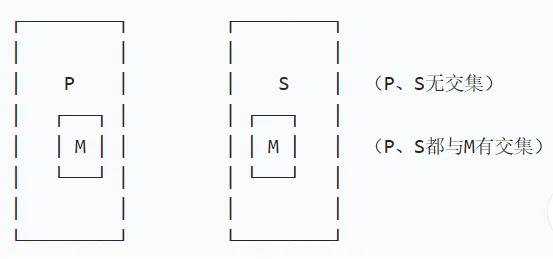
示例:
大前提:所有偶数(P)都能被 2 整除(M)
小前提:3(S)不能被 2 整除(M)
结论:3(S)不是偶数(P)
第三格:主主格:中项 M位置 在大、小前提中都是主项,推理结论必为特称判断
推理模型:所有 M 都属于 P,所有 M 都属于 S → 有些 S 属于 P
大中小项的外延关系
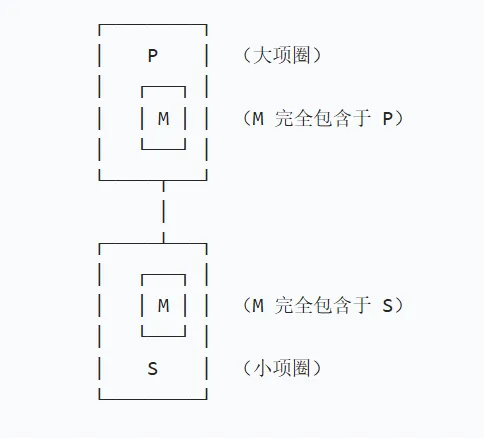
示例:
大前提:所有猫(M)都是哺乳动物(P)
小前提:所有猫(M)都是胎生动物(S)
结论:有些胎生动物(S)是哺乳动物(P)
第四格:谓主格:中项 M 在大前提中是谓项,在小前提中是主项,这种模式在日常推理中较少用。
推理模式:所有 P 都属于 M,所有 M 都属于 S → 有些 S 属于 P
大中小项的外延关系:
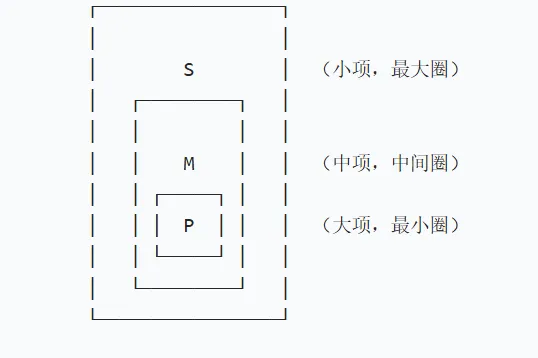
示例:
大前提:所有菱形(P)都是平行四边形(M)
小前提:所有平行四边形(M)都是四边形(S)
结论:有些四边形(S)是菱形(P)