n
9.2.4 总体离散程度的估计
[学习目标] 1.结合实例,能用样本估计总体的离散程度.2.理解方差、标准差的含义,会计算方差和标准差.(重点)3.掌握求分层随机抽样总样本的平均数及方差的方法.(难点)
导语
平均数、中位数和众数为我们提供了一组数据的集中趋势的信息,这是概括一组数据的特征的有效方法.但仅知道集中趋势的信息,很多时候还不能使我们做出有效决策.这节课我们共同来研究总体离散程度的有关知识.
一、方差、标准差
问题1假设一组数据是x1,x2,…,xn,用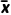 表示这组数据的平均数.我们可以怎样刻画这组数据的离散程度?
表示这组数据的平均数.我们可以怎样刻画这组数据的离散程度?
提示 用这组数据与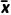 的平均距离
的平均距离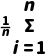 |xi-
|xi-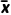 |来刻画数据的离散程度.
|来刻画数据的离散程度.
问题2如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为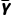 ,那么总体方差和总体标准差该如何求?
,那么总体方差和总体标准差该如何求?
提示S2=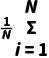 (Yi-
(Yi-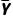 )2为总体方差,S=
)2为总体方差,S=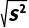 为总体标准差.
为总体标准差.
问题3方差、标准差与数据的离散程度或波动幅度有怎样的关系?
提示 标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在解决实际问题中,一般多采用标准差.
知识梳理
1.假设一组数据为x1,x2,…,xn,则这组数据的平均数为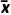 =
=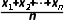 ,方差为s2=
,方差为s2=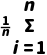 (xi-
(xi-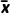 )2,标准差为s=
)2,标准差为s=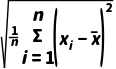 .
.
2.如果总体中所有个体的变量值分别为Y1,Y2,…,YN,总体平均数为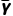 ,则称S2=
,则称S2=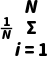 (Yi-
(Yi-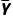 )2为总体方差,S=
)2为总体方差,S=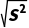 为总体标准差.
为总体标准差.
3.总体方差的加权形式:如果总体的N个变量值中,不同的值共有k(k≤N)个,不妨记为Y1,Y2,…,Yk,其中Yi出现的频数为fi(i=1,2,…,k),则总体方差为S2=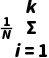 fi(Yi-
fi(Yi-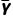 )2.
)2.
例1甲、乙两机床同时加工直径为100mm的零件,为检验质量,从中各抽取6件测量,数据为
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
解(1)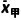 =
=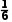 ×(99+100+98+100+100+103)=100,
×(99+100+98+100+100+103)=100,
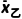 =
=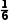 ×(99+100+102+99+100+100)=100.
×(99+100+102+99+100+100)=100.
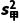 =
=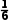 ×[(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+(103-100)2]=
×[(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+(103-100)2]=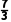
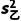 =
=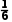 ×[(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+(100-100)2]=1.
×[(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+(100-100)2]=1.
(2)因为两台机床所加工零件的直径的平均数相同,又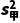 >,所以乙机床加工零件的质量更稳定.
>,所以乙机床加工零件的质量更稳定.
反思感悟在实际问题中,仅靠平均数不能完全反映问题,还要研究方差,方差描述了数据相对平均数的离散程度.在平均数相同的情况下,方差越大,离散程度越大,数据波动性越大,稳定性越差;方差越小,数据越集中,越稳定.
跟踪训练1某餐厅推出了以下两种套餐.
A套餐(在下列食品中6选2)
西式面点:蔓越莓核桃包、南瓜芝士包、黑列巴、全麦吐司.
中式面点:豆包、桂花糕.
B套餐:酱牛肉、老味烧鸡熟食类组合.
某一周两种套餐的日销售量(单位:份)如表所示.
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
A套餐 | 11 | 12 | 14 | 18 | 22 | 19 | 23 |
B套餐 | 6 | 13 | 15 | 15 | 37 | 20 | 41 |
根据上面一周的销量,分别计算A套餐和B套餐销量的平均数和方差,并根据所得数据评价两种套餐的销售情况.
解A套餐销量的平均数
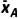 =
=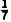 ×(11+12+14+18+22+19+23)=17,
×(11+12+14+18+22+19+23)=17,
方差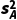 =
=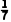 ×(62+52+32+12+52+22+62)
×(62+52+32+12+52+22+62)
=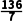 .
.
B套餐销量的平均数
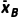 =
=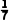 ×(6+13+15+15+37+20+41)=21,
×(6+13+15+15+37+20+41)=21,
方差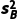 =
=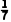 ×(152+82+62+62+162+12+202)=
×(152+82+62+62+162+12+202)=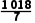 .因为
.因为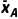 <
<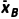 <
<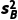
所以该周A套餐比B套餐平均销量低,但A套餐的销量比B套餐相对稳定.
二、方差、标准差与统计图表的综合应用
例2甲、乙两人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
(1)分别求出两人得分的平均数与方差;
(2)根据图形和(1)中计算结果,对两人的训练成绩作出评价.
解(1)由题图可得,甲、乙两人五次测试的成绩分别为
甲:10,13,12,14,16;
乙:13,14,12,12,14.
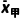 =
=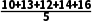 =13,
=13,
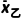 =
=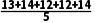 =13,
=13,
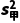 =
=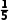 ×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
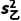 =
=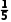 ×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
(2)由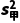 >
>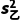 可知乙的成绩较稳定.
可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
反思感悟折线统计图中数字特征的求解技巧
根据折线统计图研究样本数据的数字特征与横坐标和纵坐标的统计意义有关,但一般情况下,整体分布位置较高的平均数大,数据波动性小的方差小.
跟踪训练2 甲、乙、丙三名学生在一项集训中的40次测试分数都在[50,100]内,将他们的测试分数分别绘制成频率分布直方图,如图所示,记甲、乙、丙的分数标准差分别为s1,s2,s3,则它们的大小关系为( )
A.s1>s2>s3B.s1>s3>s2
C.s3>s1>s2D.s3>s2>s1
答案 B
解析比较三个频率分布直方图知,甲为“双峰”直方图,两端数据最多,最分散,标准差最大;乙为“单峰”直方图,数据最集中,标准差最小;丙为“单峰”直方图,但数据分布相对均匀,标准差介于甲、乙之间.综上可知s1>s3>s2.
三、分层随机抽样的方差
问题4分层随机抽样的方差如何计算?
提示 对于按比例分配的分层随机抽样的样本数据,设样本量为n,平均数为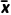 ,若总体分为两层,两层的个体数量分别为n1,n2,两层的平均数分别为
,若总体分为两层,两层的个体数量分别为n1,n2,两层的平均数分别为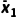 ,方差分别为
,方差分别为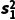 ,则这个样本的方差为s2=
,则这个样本的方差为s2=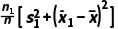 +
+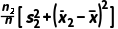 .
.
知识梳理
假设第一层有m个数,分别为x1,x2,…,xm,平均数为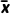 ,方差为s2;第二层有n个数,分别为y1,y2,…,yn,平均数为
,方差为s2;第二层有n个数,分别为y1,y2,…,yn,平均数为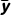 ,方差为t2.则
,方差为t2.则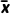 =
=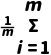 xi,s2=
xi,s2=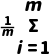 (xi-
(xi-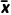 )2,=
)2,=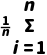 yi,
yi,
t2=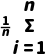 (yi-
(yi-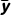 )2.
)2.
若记总的样本平均数为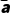 ,样本方差为b2,则可以算出
,样本方差为b2,则可以算出
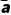 =
=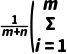 xi+
xi+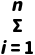 yi)=
yi)=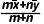
b2=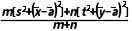
=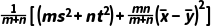 .
.
例3坐位体前屈是中小学体质健康测试项目,主要测试学生躯干、腰、髋等部位关节韧带和肌肉的伸展性、弹性及身体柔韧性.在对某高中1500名高三年级学生的坐位体前屈成绩的调查中,采用按学生性别比例分配的分层随机抽样的方法抽取100人,已知这1500名高三年级学生中男生有900人,且抽取的样本中男生的平均数和方差分别为13.2cm和13.36,女生的平均数和方差分别为15.2cm和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高三年级全体学生的坐位体前屈成绩的方差.
参考公式:总体分为2层,按比例分配的分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为n1,,,n2,,.记总样本的平均数为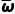 ,样本方差为s2,s2=
,样本方差为s2,s2=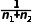 {n1[
{n1[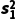 +(
+(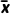 -
-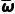 )2]+n2[
)2]+n2[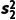 +(
+(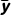 -
-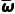 )2]}.
)2]}.
解(1)设在男生、女生中分别抽取n1名和n2名,则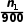 =
=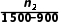 =
=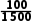
解得n1=60,n2=40.
记抽取的总样本的平均数为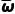 ,根据按比例分配的分层随机抽样的总样本平均数与各层样本平均数的关系,
,根据按比例分配的分层随机抽样的总样本平均数与各层样本平均数的关系,
可得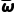 =
=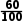 ×13.2+
×13.2+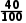 ×15.2=14(cm).
×15.2=14(cm).
所以抽取的总样本的平均数为14cm.
(2)男生样本的平均数为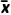 =13.2cm,
=13.2cm,
样本方差为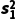 =13.36;
=13.36;
女生样本的平均数为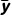 =15.2cm,
=15.2cm,
样本方差为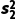 =17.56.
=17.56.
由(1)知,总样本的平均数为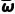 =14cm.
=14cm.
记总样本方差为s2,
则s2=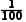 {60×[13.36+(13.2-14)2]+40×[17.56+(15.2-14)2]}=16.
{60×[13.36+(13.2-14)2]+40×[17.56+(15.2-14)2]}=16.
所以估计高三年级全体学生的坐位体前屈成绩的方差为16.
反思感悟有n个个体的样本中不同层的平均数记为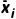 (i=1,2,…,k,k≤n),方差记为
(i=1,2,…,k,k≤n),方差记为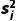 ,相应各层个体的个数记为fi,则样本的平均数
,相应各层个体的个数记为fi,则样本的平均数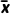 =
=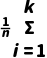 fi
fi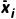 ,方差s2=
,方差s2=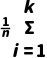 fi
fi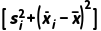 .
.
跟踪训练3甲、乙两支田径队队员的体检结果为:甲队队员体重的平均数为60kg,方差为200,乙队队员体重的平均数为70kg,方差为300,已知甲、乙两队的队员人数之比为1∶4,求甲、乙两队全部队员体重的平均数和方差.
解由题意可知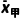 =60kg,甲队队员在所有队员中所占权重为
=60kg,甲队队员在所有队员中所占权重为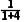 =
=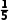
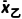 =70kg,乙队队员在所有队员中所占权重为
=70kg,乙队队员在所有队员中所占权重为
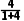 =
=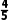 ,则甲、乙两队全部队员体重的平均数
,则甲、乙两队全部队员体重的平均数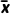 =
=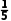 ×60+
×60+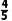 ×70=68(kg),
×70=68(kg),

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享