n
培优课 与球有关的内切、外接问题
[学习目标] 1.掌握简单几何体的外接球问题的求解方法.(重点)2.会求特殊几何体的内切球的相关问题.(难点)
导语
与球有关的内切、外接问题是立体几何的一个重点(切、接问题的解题思路类似,此处以多面体的外接球为例).研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系.
一、直接法
例1(1)一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为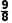 ,一个底面的周长为3,则这个球的体积为.
,一个底面的周长为3,则这个球的体积为.
答案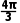
解析设正六棱柱的底面边长为x,高为h,
则有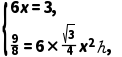 ∴
∴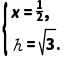
∴正六棱柱的底面外接圆的半径r=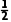
球心到底面的距离d=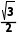 .
.
∴外接球的半径R=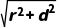 =1.∴V球=
=1.∴V球=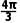 .
.
(2)在三棱锥A-BCD中,侧棱长均为2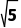 ,底面是边长为2
,底面是边长为2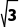 的等边三角形,则该三棱锥外接球的体积为.
的等边三角形,则该三棱锥外接球的体积为.
答案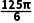
解析由题意知该三棱锥为正三棱锥,如图所示,O为底面△BCD的中心且AO垂直于底面△BCD,O'在线段AO上,O'为外接球球心,
令O'A=O'D=R,
∵OD=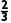 DE=
DE=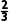 ×2
×2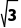 ×
×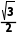 =2,AD=2
=2,AD=2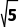
∴AO=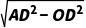 =4,
=4,
∴OO'=4-R,
又OO'2+OD2=O'D2,
∴(4-R)2+4=R2,解得R=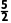
∴V球=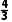 πR3=
πR3=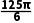 .
.
反思感悟找几何体的外接球球心,即找点O,使点O与几何体各顶点的距离相等.正棱锥的外接球球心在底面的垂线上,直棱柱的外接球球心为上、下底面外心所连线段的中点.
跟踪训练1正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.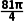 B.16πC.9πD.
B.16πC.9πD.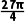
答案 A
解析如图,设球心为O,半径为r,AE=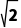 =4-r,则在Rt△AOE中,(4-r)2+(
=4-r,则在Rt△AOE中,(4-r)2+(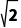 )2=r2(或(r-4)2+(
)2=r2(或(r-4)2+(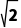 )2=r2),解得r=
)2=r2),解得r=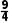 ,
,
∴该球的表面积为4πr2=4π×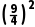 =
=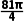 .
.
二、构造法
例2(1)三棱锥A-BCD的四个面都是直角三角形,且侧棱AB垂直于底面BCD,BC⊥CD,AB=BC=2,且V三棱锥A-BCD=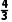 ,则该三棱锥A-BCD外接球的体积为.
,则该三棱锥A-BCD外接球的体积为.
答案 4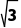 π
π
解析因为AB⊥BC,BC⊥CD,构造如图所示的长方体,
则AD为三棱锥A-BCD的外接球的直径.设外接球的半径为R.
∵V三棱锥A-BCD=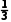 ×
×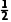 ×BC×CD×AB
×BC×CD×AB
=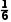 ×2×CD×2=
×2×CD×2=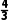
∴CD=2,∴该长方体为正方体,
∴AD=2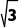 R=
R=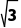
故外接球的体积为V=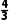 πR3=4
πR3=4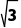 π.
π.
延伸探究若把条件改为三棱锥A-BCD的三个面是直角三角形,且侧棱AB垂直于底面BCD,BC⊥BD,AB=BC=2,且V三棱锥A-BCD=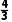 ,则该三棱锥A-BCD外接球的体积为.
,则该三棱锥A-BCD外接球的体积为.
答案 4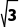 π
π
解析因为AB⊥BC,AB⊥BD,BC⊥BD,
构造如图所示的长方体,
则AE为三棱锥A-BCD的外接球的直径,
设外接球的半径为R.
V三棱锥A-BCD=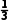 ×
×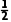 ×BC×BD×AB
×BC×BD×AB
=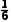 ×2×BD×2=
×2×BD×2=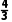
∴BD=2,∴该长方体为正方体,
∴AE=2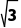 R=
R=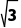
∴外接球的体积为V=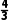 πR3=4
πR3=4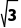 π.
π.
(2)“阿基米德多面体”也称为半正多面体,是由边数不全相同的正多边形围成的多面体,它体现了数学的对称美.如图所示,将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥,共可截去八个三棱锥,得到八个面为正三角形、六个面为正方形的一种阿基米德多面体.已知AB=1,则关于图中的半正多面体,下列说法正确的有( )
A.该半正多面体的体积为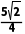
B.该半正多面体过A,B,C三点的截面面积为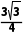
C.该半正多面体外接球的表面积为8π
D.该半正多面体的表面积为6+2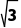
答案 D
解析如图,因为AB=1,
所以该半正多面体是由棱长为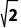 的正方体沿各棱中点截去八个三棱锥所得到的,
的正方体沿各棱中点截去八个三棱锥所得到的,
所以该半正多面体的体积V=(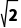 )3-8×
)3-8×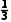 ×
×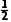 ×
×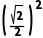 ×
×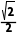 =
=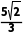 ,故A错误;
,故A错误;
根据该半正多面体的对称性可知,过A,B,C三点的截面为正六边形ABCFED,
又AB=1,所以正六边形的面积S=6×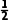 ×1×1×
×1×1×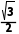 =
=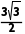 ,故B错误;
,故B错误;
根据该半正多面体的对称性可知,该半正多面体的外接球的球心为正方体的中心,
即正六边形ABCFED的中心,故半径R=1,
所以该半正多面体外接球的表面积为S=4πR2=4π×12=4π,故C错误;
因为该半正多面体的八个面为正三角形、六个面为正方形,棱长皆为1,
所以其表面积为8×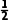 ×1×1×
×1×1×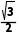 +6×12=6+2
+6×12=6+2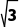 ,故D正确.
,故D正确.
反思感悟构造法的解题策略
(1)侧面为直角三角形的四面体或正四面体,或对棱均相等的模型,可以放到正方体或长方体中去求解.
①若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.
②若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.
③正四面体P-ABC可以补形为正方体且正方体的棱长a=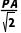 ,如图3所示.
,如图3所示.
④若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示.
(2)将直三棱锥补成三棱柱求解.
跟踪训练2三棱锥P-ABC的三条侧棱两两垂直,三个侧面的面积分别是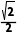 ,则该三棱锥的外接球的体积是( )
,则该三棱锥的外接球的体积是( )
A.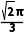 B.
B.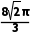 C.
C.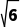 πD.8
πD.8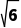 π
π
答案 C
解析三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享