前面学习了使用函数来表示状态值的处理方式。
此处基于参考资料中的以下章节,学习使用函数(用神经网络近似)来表示策略,并通过神经网络的参数更新求解最优策略。
基础概念
对于网格世界等这种简单环境,常用表格法来表示策略。
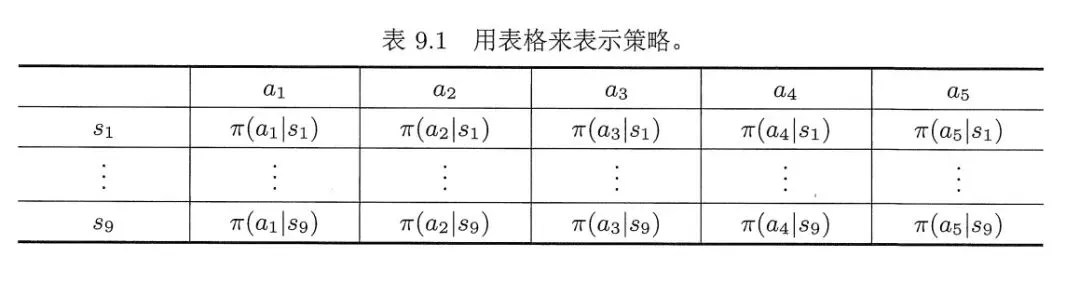
如果状态和动作过多,可以使用函数来表示策略。
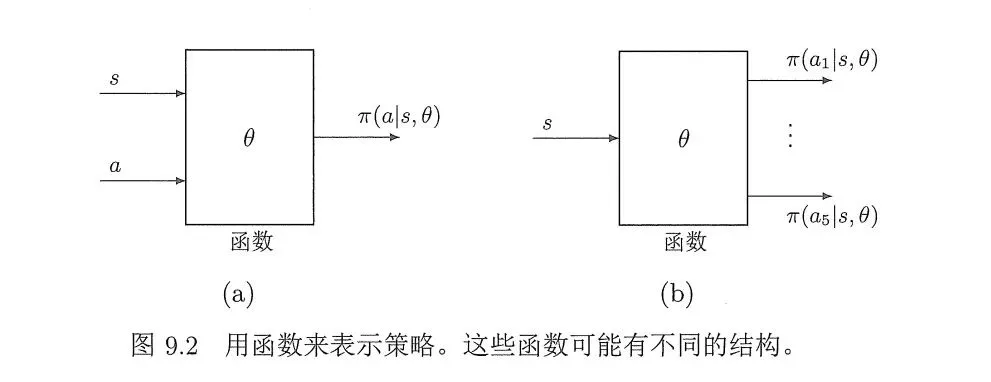
如果函数(比如神经网络这种非线性函数)来表示策略,其目标函数基于参考资料3如下。
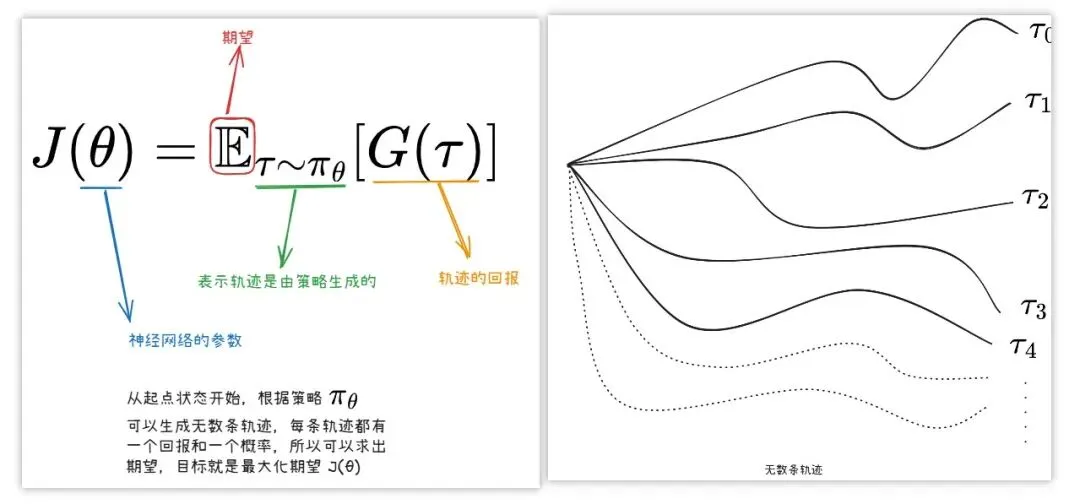
先获得目标函数的梯度,通过梯度上升法优化参数来最大化目标函数(可能的轨迹有无数条,一般采样n条求平均)。
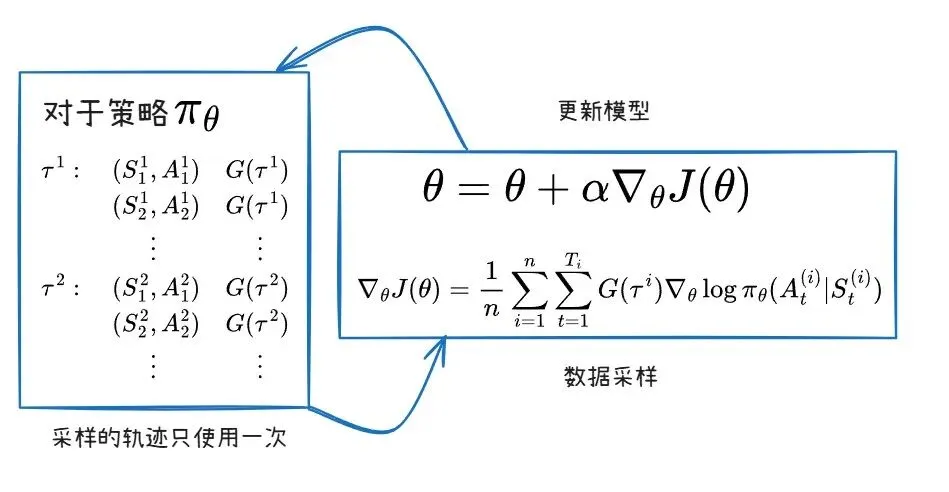
对于回报G(T)的计算方式不同,有REINFORCE和Actor-Critic(演员-评论家)两种经典算法。

REINFORCE算法
参考资料2第9章给出了车杆环境使用REINFORCE算法求解的案例。
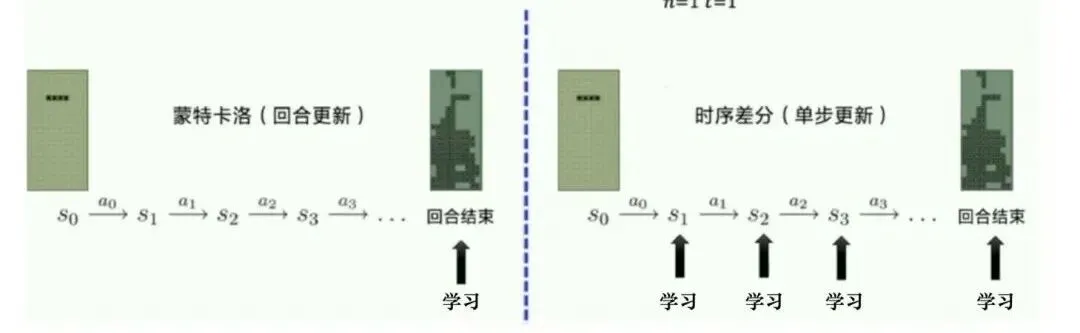
最简单的策略梯度法中,回报G(T)是整条轨迹的回报,作为权重项乘以每个时刻的策略梯度。
REINFORCE算法中G(T)修正为各时刻的回报而非整条完整轨迹的回报。从代码上可以区分两者。
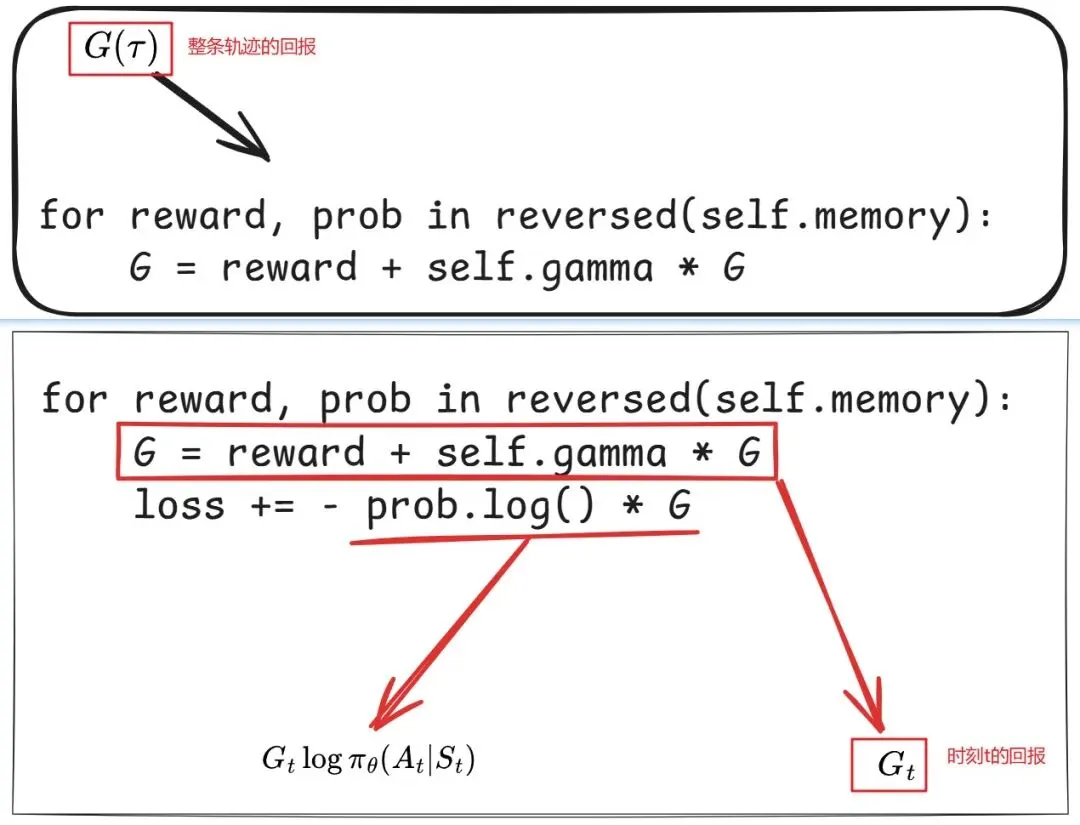
基于参考资料2的9.3节,算法流程如下。
将损失函数设置为目标函数的负数,复用梯度下降法来更新参数。

根据轨迹中的样本,不断调整网络参数,使得回报大的动作概率调升进而优化策略。

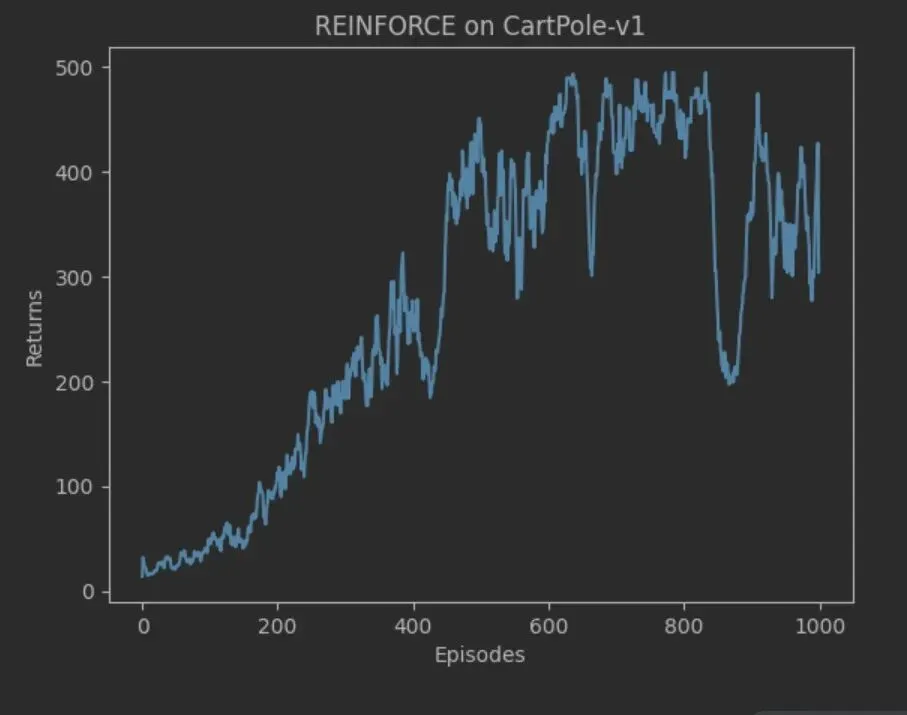
程序采样1千个轨迹后,轨迹的回报逐步增加到环境最高值500。回报随着每次采集的新样本而产生波动。
Actor-Critic(演员-评论家)算法
策略梯度数据形式较多,参考资料2的Actor-Critic案例可以认为是下图中的第(6)种形式。
第(6)种形式中,用状态函数作为基线函数以区分不同策略的效果,并使用时序差分方法来估计动作值,整体表达式即为时序差分算法中的误差项。

可以使用一个神经网络来表示此价值函数,设置误差项为损失函数,基于样本数据不断调整网络参数,使得误差越来越小。即估计的状态值越来越准确,且这个时序差分误差作为梯度权重来指导策略更新——正向强化好的动作,负向抑制坏的动作。
所以算法的Actor部分通过策略网络输出动作概率分布,Critic部分通过价值网络计算时序差分误差指导Actor更新。

参考资料2第10章给出了车杆环境使用Actor-Critic算法求解的案例。
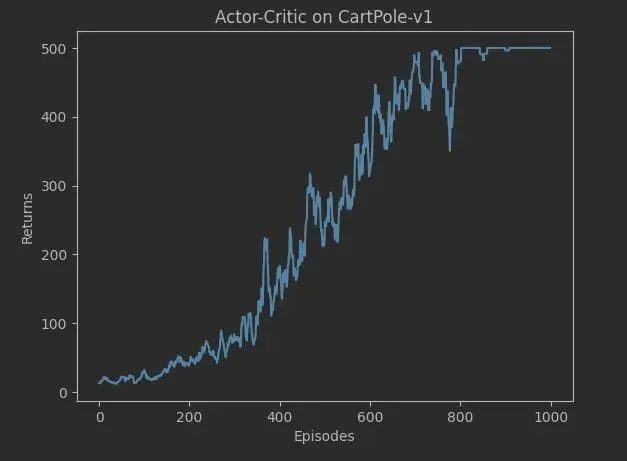
程序运行1千个轨迹后,轨迹的回报逐步增加到环境最高值500。且相比上面的REINFORCE算法结果,收敛更稳定。
参考资料1-3中给出较多的Actor-Critic(演员-评论家)算法扩展,待后续探究。
参考
- 2. 张伟楠、沈键、俞勇等《动手学强化学习》人民邮电出版社
- 3. 王琦、杨毅远、江季等《Easy RL :强化学习教程》人民邮电出版社