【26版步步高高中数学人教A版必修二学习笔记第八章习题课异面直线所成的角及直线与平面所成的角的解法

n

习题课　异面直线所成的角及直线与平面所成的角的解法

［学习目标］　1.理解异面直线所成的角的概念，会运用平移的方法求异面直线所成的角.(重点)2.掌握直线与平面所成角的求法.(难点)

一、异面直线所成的角

例1已知圆锥的顶点为P，底面圆心为O，母线长为6，PO=4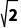是底面半径，且OA⊥OB，M为线段AB的中点，如图所示.求异面直线PM与OB所成角的余弦值.

解如图，取OA的中点N，连接PN，MN，OM，

因为N为OA的中点，M为AB的中点，所以MN∥OB，

于是∠PMN(或其补角)是异面直线PM与OB所成的角.

因为M为AB的中点，

OA=OB=2，且OA⊥OB，

则OM=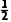AB=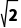

又PN===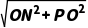

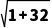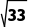
PM===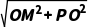

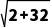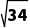
所以cos∠PMN=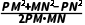

==

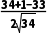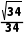
则异面直线PM与OB所成角的余弦值为.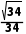

反思感悟求异面直线所成的角的方法

可通过多种方法平移产生三角形，主要有三种方法：(1)直接平移法(可利用图中已有的平行线)；(2)中位线平移法；(3)补形平移法(在已知图形中，补作一个相同的几何体，以便找到平行线).

跟踪训练1如图，已知在三棱锥A-BCD中，AD=1，BC=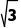，且AD⊥BC，BD=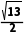=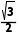，求异面直线AC与BD所成角的大小.

解取AB，AD，DC，BD的中点分别为E，F，G，M，连接EF，FG，GM，ME，EG.

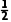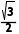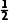则MG=BC==AD=.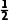

因为AD⊥BC，所以EM⊥MG.

在Rt△EMG中，

EG=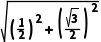=1.

由题图可知，∠EFG(或补角)为异面直线AC与BD所成的角.

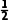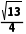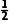在△EFG中，因为EF=BD==AC=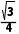，且EF²+FG²=EG²，所以EF⊥FG，

即AC⊥BD.

所以异面直线AC与BD所成的角为90°.

二、直线与平面所成的角

例2如图，在三棱锥P-ABC中，PA=AC=BC，PA⊥平面ABC，∠ACB=90°，O为PB的中点，求直线CO与平面PAC所成角的余弦值.

解如图，取PC的中点为E，连接EO，则OE∥BC.

∵PA⊥平面ABC，BC⊂平面ABC，

∴PA⊥BC.又AC⊥BC，AC∩PA=A，PA，AC⊂平面PAC，

∴BC⊥平面PAC.又OE∥BC，

∴OE⊥平面PAC，

∴∠OCE为直线CO与平面PAC所成的角.

设PA=AC=BC=2，则OE=1，CE==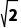

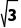
∴cos∠OCE==.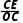

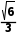∴直线CO与平面PAC所成角的余弦值为.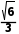

反思感悟求斜线和平面所成的角的步骤

(1)作(或找)：作(或找)出斜线在平面上的射影，作射影要过斜线上斜足以外的一点作平面的垂线，再过垂足和斜足作直线，注意斜线上点的选取以及垂足的位置要与题目中已知量有关，这样才能便于计算.

(2)证：证明某平面角就是斜线和平面所成的角.

(3)算：通常在垂线段、斜线和射影所组成的直角三角形中计算.

跟踪训练2已知正三棱锥的侧棱长是底面边长的2倍，求侧棱和底面所成角的余弦值.

解如图，设正三棱锥S-ABC的底面边长为a，则侧棱长为2a.

设O为底面△ABC的中心，

则∠SAO为SA和平面ABC所成的角.在Rt△SOA中，

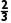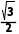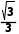因为AO=×a=a，

所以cos∠SAO===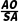

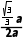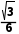
即侧棱和底面所成角的余弦值为.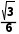

三、折叠问题

例3　如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，将△ADE沿DE折起到△A₁DE的位置，使A₁D⊥DC，如图2.

(1)求证：BC⊥平面A₁CD；

(2)当AD的长为多少时，异面直线DE，A₁B所成的角最小？求出此时所成角的余弦值.

(1)证明在题图2中，因为A₁D⊥DE，A₁D⊥DC，DE∩DC=D，DE，DC⊂平面BCDE，

所以A₁D⊥平面BCDE.

又BC⊂平面BCDE，所以A₁D⊥BC.

又BC⊥DC，A₁D∩DC=D，

A₁D，DC⊂平面A₁CD，

所以BC⊥平面A₁CD.

(2)解连接DB(图略)，设AD=A₁D=x，

则DC=6-x，0<x<6.由(1)得BC⊥A₁C，

A₁D⊥DB，

在Rt△BCD中，DB²=DC²+BC²=(6-x)²+3²=x²-12x+45，

所以在Rt△A₁DB中，A₁B===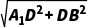

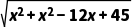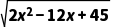
显然，当x=3，即AD=3(或D为AC的中点)时，线段A₁B的长取得最小值，最小值是3.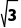

因为BC∥ED，所以∠A₁BC即为异面直线DE，A₁B所成的角，

在Rt△A₁CB中，

cos∠A₁BC==≤=.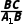

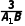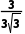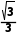因为余弦函数在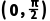上单调递减，所以当cos∠A₁BC取最大值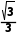时，∠A₁BC最小.

综上，当AD=3时，异面直线DE，A₁B所成的角最小，此时所成角的余弦值为.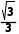

反思感悟折叠问题在空间几何中主要看折叠前后哪些量保持不变，哪些量发生改变.

跟踪训练3如图1，在矩形ABCD中，AB=3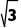=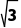，沿对角线BD将△BCD折起到△BPD的位置，且P在平面ABD上的射影O恰好在AB上，如图2.

(1)求证：PB⊥平面PAD；

(2)求点A到平面BPD的距离；

(3)求直线AB与平面PBD所成角的正弦值.

(1)证明∵点P在平面ABD上的射影O在AB上，

∴PO⊥平面ABD，DA⊂平面ABD，

∴PO⊥DA.

又∵AD⊥AB，AB∩PO=O，

AB，PO⊂平面ABP，

∴DA⊥平面ABP，又BP⊂平面ABP，

∴DA⊥BP.

又∵BC⊥CD，∴BP⊥PD.

∵DA∩PD=D，DA，PD⊂平面APD，

∴BP⊥平面APD.

(2)解如图所示，过A作AE⊥PD，垂足为E，连接BE.

∵BP⊥平面APD，

AE⊂平面APD，

∴BP⊥AE，又BP∩PD=P，

BP，PD⊂平面BPD，∴AE⊥平面BPD.

故AE的长就是点A到平面BPD的距离.

又DA⊥平面ABP，AP⊂平面ABP，

∴DA⊥AP.

在Rt△APB中，AP=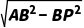=2.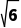

通过网盘分享的文件：同步PPT课件等3个文件

链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321 

--来自百度网盘超级会员v8的分享