n
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定定理
[学习目标] 1.理解二面角及其平面角的概念并掌握二面角的平面角的一般作法,会求简单的二面角的平面角.(重点、难点)2.掌握两个平面互相垂直的概念,能用定义和定理判定面面垂直.(重点)3.能利用面面垂直的判定定理解决一些综合问题.(难点)
导语
回顾两条直线垂直的定义,要先定义角的概念,利用两条直线所成角的特殊情况研究直线垂直,因此,定义两平面垂直,我们先从二面角开始.
一、二面角的概念
问题1 你能举出哪些两个平面相交的例子?
提示 卫星的轨道平面与地球的赤道平面、教室的墙面与地面等等.
问题2 我们通常说“把门开大一些”(动手演示教室的门),是指哪个角大一些?如何去刻画二面角的大小呢?
提示 指门与门框所成的二面角大一些.取二面角棱l上的一点O在二面角的面上分别作射线OA,OB与二面角的棱垂直,得到∠AOB可以刻画二面角.
问题3 ∠AOB的大小与点O在棱l上的位置有关吗?
提示 无关.
知识梳理
1.二面角的定义
从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
2.画法:
3.记法:二面角α-l-β或二面角α-AB-β或二面角P-l-Q或二面角P-AB-Q.
4.二面角的平面角
(1)在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角,如图.
(2)二面角的平面角α的取值范围是0°≤α≤180°.平面角是直角的二面角叫做直二面角.
例1已知四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(1)二面角B-PA-D的平面角的大小;
(2)二面角B-PA-C的平面角的大小;
(3)二面角A-PD-C的平面角的大小.
解(1)∵PA⊥平面ABCD,AB⊂平面ABCD,AD⊂平面ABCD,
∴AB⊥PA,AD⊥PA.
∴∠BAD为二面角B-PA-D的平面角.
又四边形ABCD为正方形,∴∠BAD=90°,
∴二面角B-PA-D的平面角为90°.
(2)∵PA⊥平面ABCD,AB⊂平面ABCD,
AC⊂平面ABCD,
∴AB⊥PA,AC⊥PA.
∴∠BAC为二面角B-PA-C的平面角.
又四边形ABCD为正方形,∴∠BAC=45°.
即二面角B-PA-C的平面角为45°.
(3)如图,取PD,PC的中点分别为O,M,连接AO,MO,
∵PA⊥平面ABCD,AD,CD⊂平面ABCD,
∴PA⊥AD,PA⊥CD,
又PA=AB=AD,∴AO⊥PD.
∵PA⊥CD,又AD⊥CD,
AD,PA⊂平面PAD,AD∩PA=A,
∴CD⊥平面PAD,
又PD⊂平面PAD,
∴CD⊥PD,又∵OM∥CD,
∴OM⊥PD,OM⊥平面PAD,
∴OM⊥OA,又∵PD是二面角A-PD-C的棱,
∴∠AOM为二面角A-PD-C的平面角,即为90°.
反思感悟(1)确定二面角的平面角的方法
①定义法:在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.
②垂面法:过棱上一点作与棱垂直的平面,该平面与二面角的两个半平面相交产生两条射线,这两条射线所成的角,即为二面角的平面角.
③垂线法:如果两个平面相交,有过一个平面内的一点与另一个平面垂直的垂线,可过这一点作棱的垂线,连接两个垂足,应用直线与平面垂直的判定定理可证明连线与棱垂直,找到二面角的平面角.
(2)求二面角大小的步骤
①找出这个平面角.
②证明这个角是二面角的平面角.
③作出这个角所在的三角形,解这个三角形,求出角的大小.
跟踪训练1如图,AB是☉O的直径,PA垂直于☉O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.
解由已知得PA⊥平面ABC,BC⊂平面ABC,
∴PA⊥BC.
∵AB是☉O的直径,且点C在圆周上,∴AC⊥BC.
又PA∩AC=A,PA,AC⊂平面PAC,
∴BC⊥平面PAC.
又PC⊂平面PAC,∴PC⊥BC.
又BC是二面角P-BC-A的棱,
∴∠PCA是二面角P-BC-A的平面角.
由PA=AC知△PAC是等腰直角三角形.
∴∠PCA=45°,故二面角P-BC-A的大小为45°.
二、平面与平面垂直的定义及应用
问题4教室相邻的两个墙面与地面可以构成几个二面角?这些二面角的大小是多少?
提示 可以构成3个二面角,分别是两相邻墙面构成的二面角,一个墙面与地面构成的二面角,另一个墙面与地面构成的二面角.它们构成的二面角是直二面角,即二面角的度数为90°.
知识梳理
平面与平面垂直的定义与画法
(1)定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,记作:α⊥β.
(2)画法:
例2如图所示,在四面体A-BCD中,BD=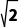 a,AB=AD=CB=CD=AC=a.
a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD.
证明∵AB=AD=CB=CD=a,
∴△ABD与△BCD是等腰三角形.
取BD的中点E,连接AE,CE,如图,
则AE⊥BD,BD⊥CE.
∴∠AEC为二面角A-BD-C的平面角.
在Rt△ABD中,AB=a,
BE=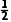 BD=
BD=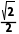 a,∴AE=
a,∴AE=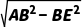 =
=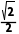 a.
a.
同理CE=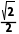 a.
a.
在△AEC中,AE=CE=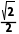 a,AC=a,
a,AC=a,
∴AC2=AE2+CE2,
∴AE⊥CE,即∠AEC=90°,
即二面角A-BD-C的平面角为90°.
∴平面ABD⊥平面BCD.
反思感悟用定义证明两个平面垂直的步骤

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享