【26版步步高高中数学人教A版必修二学习笔记第六章6.4.3第3课时余弦定理、正弦定理的综合运用

n

第3课时　余弦定理、正弦定理的综合运用

［学习目标］　1.利用正弦、余弦定理判断三角形的形状.(重点)2.理解三角形面积公式的推导过程，掌握三角形的面积公式.(重点)3.掌握正弦、余弦定理与三角函数的综合应用.(难点)

一、利用正弦、余弦定理判断三角形的形状

例1在△ABC中，若acos A=bcos B，试判断△ABC的形状.

解方法一由正弦定理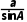=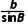，得=.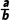

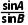又acosA=bcosB，∴=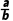

∴=

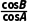
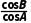
∴sinAcosA=sinBcosB，

∴2sinAcosA=2sinBcosB，即sin2A=sin2B，

∵A，B为三角形内角，

∴2A=2B或2A+2B=π，即A=B或A+B=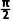ABC是等腰三角形或直角三角形.

方法二由已知及余弦定理，得

a·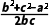=b·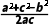

∴a²(b²+c²-a²)=b²(a²+c²-b²)，

即a²b²+a²c²-a⁴=b²a²+b²c²-b^4，

∴a²c²-b²c²-(a⁴-b⁴)=0，

∴(a²-b²)［c²-(a²+b²)］=0，

从而a²-b²=0或c²-(a²+b²)=0，

即a=b或c²=a²+b^2，

∴△ABC是等腰三角形或直角三角形.

延伸探究若把本例中“acosA=bcosB”改为“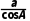=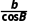”，试判断△ABC的形状.

解由正弦定理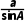=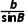，得=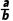

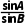
又==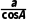

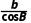
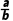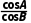
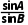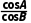∴=，即sinAcosB-cosAsinB=0，

∴sin(A-B)=0，

∵-π<A-B<π，∴A-B=0，∴A=B，

∴△ABC为等腰三角形.

反思感悟判断三角形形状的方法及注意事项

(1)利用正弦定理、余弦定理把已知条件转化为边(或角)的关系，通过因式分解、配方等得出边(或角)的相应关系，从而判断三角形的形状.

(2)通过变形得到边(或角)的关系后，如果等式两侧或同侧有公因式，注意不要轻易约分，应先移项再提取公因式，以免漏解.

(3)常见的特殊三角形有正三角形、等腰三角形、直角三角形等，要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.

跟踪训练1已知a，b，c分别为△ABC内角A，B，C的对边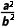，=，则△ABC的形状是(　　)

A.直角三角形

B.等腰三角形

C.等腰直角三角形

D.直角三角形或等腰三角形

答案　D

解析因为=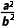

所以a²tanB=b²tanA，

所以由正弦定理，得sin²AtanB=sin²BtanA，

即sin²A·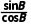=sin²B·.

在△ABC中，因为0<A<π，0<B<π，

所以sinA≠0，sinB≠0，

所以sinAcosA=sinBcosB，即sin2A=sin2B，

所以2A=2B或2A+2B=π，

即A=B或A+B=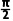

所以△ABC是等腰三角形或直角三角形.

二、三角形面积公式

问题已知△ABC的两边a，b和角C，如何求△ABC的面积？

提示　边b上的高h为asin C，故面积为S=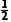bh=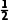absin C.

知识梳理

1.三角形的面积公式：已知△ABC的内角A，B，C所对的边分别为a，b，c，则△ABC的面积公式为S=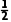absin C=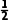bcsin A=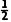casin B.

2.△ABC中的常用结论

(1)A+B+C=180°，

sin(A+B)=sin C，cos(A+B)=-cos C.

(2)大边对大角，即a>b⇔A>B ⇔sin A>sin B.

(3)任意两边之和大于第三边，任意两边之差小于第三边.

例2(1)在△ABC中，A=30°，C=45°，a=2，求S_△ABC；

(2)若△ABC的面积为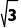=2，C=60°，求边AB的长度.

解(1)方法一因为A=30°，C=45°，

所以B=105°，

由正弦定理=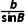

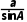
得b===+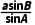

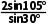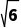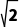
S_△ABC=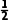absinC=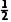×2×(+)×

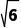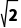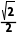
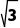=+1.

方法二设△ABC的外接圆半径为R，由正弦定理得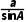==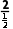4=2R，所以R=2.

又A=30°，C=45°，所以B=105°，

所以S_△ABC=2R²sinAsinBsinC=8×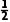××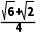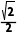=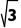+1.

(2)方法一由S_△ABC=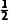AC·BC·sinC=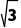

得AC=2，

由余弦定理，得AB²=AC²+BC²-2AC·BC·cos60°=2²+2²-2×2×2×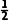=4，

所以AB=2，即边AB的长度为2.

方法二由S_△ABC=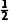AC·BC·sinC=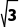

得AC=2，

所以AC=BC=2，又C=60°，

所以△ABC为等边三角形，所以AB=2，

即边AB的长度为2.

反思感悟(1)求三角形的面积时，要充分挖掘题目中的条件，通过内角和定理及解三角形等途径，求得三角形的两边及其夹角，进而利用三角形的面积公式求解.在解题过程中，要注意方程思想在解题中的应用.

(2)求三角形面积的最值时，要注意函数求最值的方法，尤其是基本不等式的应用.

跟踪训练2(1)已知在△ABC中，角A，B，C所对的边分别为a，b，c，a=8，b=7，B=60°，求c及S_△ABC.

解在△ABC中，由余弦定理

b²=a²+c²-2accosB，

得49=64+c²-16c×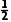

整理得c²-8c+15=0，

解得c=3或c=5.

当c=3时，

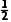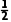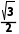S_△ABC=acsinB=×8×3×=6；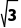

当c=5时，

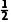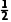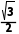S_△ABC=acsinB=×8×5×=10.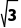

(2)设△ABC的内角A，B，C所对的边分别为a，b，c，b=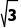，(2a-c)cos B=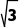cos C，则△ABC面积的最大值是.

答案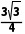

解析∵b=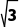

∴(2a-c)cosB=bcosC.

由正弦定理，得(2sinA-sinC)cosB=sinBcosC，

∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA，

∵A∈(0，π)，∴sinA≠0，∴cosB=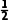

又B∈(0，π)，∴B=.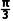

由余弦定理的推论，可得=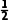

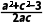
即a²+c²=3+ac≥2ac(当且仅当a=c时取等号)，∴ac≤3，

∴S_△ABC=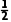acsinB≤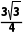

即△ABC面积的最大值为.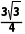

三、正弦、余弦定理的综合应用

例3在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为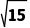-c=2，cos A=-.

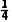(1)求a和sin C的值；

(2)求cos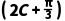的值.

解(1)在△ABC中，∵cos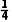A=-A∈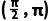

∴sinA==

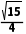
由△ABC的面积为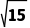，可得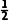bcsinA=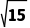

可得bc=8.

又b-c=2，解得b=4，c=2或b=-2，c=-4(舍去)，

∴b=4，c=2，

通过网盘分享的文件：同步PPT课件等3个文件

链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321 

--来自百度网盘超级会员v8的分享