最近在学习单极单相OBC相关的知识,拓扑如下图1:
虽然我想学习的是双有源桥拓扑,不过也可以先使用原边半桥分析;
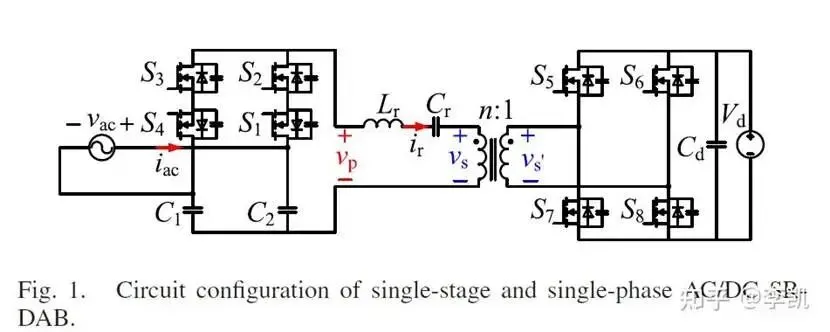
查阅了相当多的论文,发现许多的论文都是以DAB的拓扑来做的谐振腔,但是DAB来做有许多的缺点,如下图2:
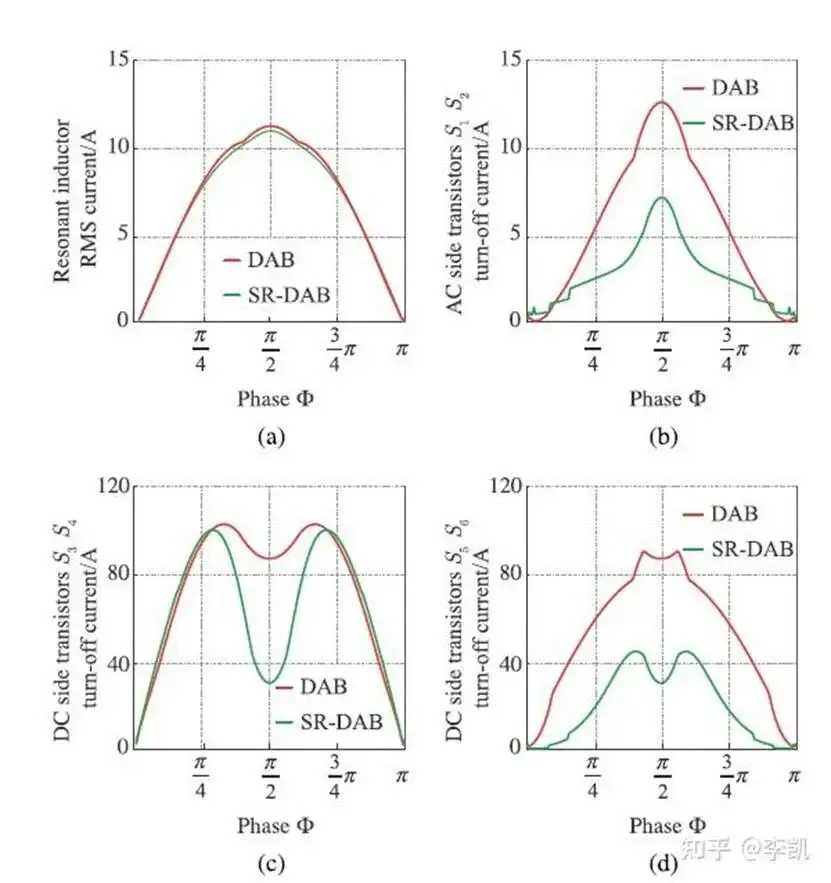
主要就是原副边的管子关断电流大,电流应力问题不好解决;
因此一些文献把传统的DAB做成了SRDAB(串联谐振DAB);
但是在SRDAB拓扑里面有许多的控制量,最多可能有四个(开关频率和三重移相);
即使按照最简单的调频加单移相控制也是两个控制目标,以前做的项目不管是LLC、移相全桥或者PFC都是频率或者占空比二选一,没有同时闭环调节两个控制目标的;
因此前一段时间我完全想不明白怎么同时调节移相角的同时调节开关频率;
查阅了一段时间的论文,发现许多的论文都太理论,
A_Bidirectional_Isolated_Dual-Phase-Shift_Variable-Frequency_Series_Resonant_Dual-Active-Bridge_GaN_ACDC_Converter
这篇文献居然需要根据运行的数据,利用matlab计算最优开关频率,这个我实在不知道工程上怎么应用。
这个文献又太复杂了,需要不断的迭代计算,我还没做来,不知道哪里出了问题;
Control of Single-Stage SR-DAB-Based Bidirectional AC/DC Converter With Simplicity and High Accuracy
看了一段时间的文献,我发现其实我对DCDC的SRDAB都没有搞明白,所以我决定从基于DCDC的SRDAB开始学习,理论上基于DCDC的SRDAB是单极OBC的一种特殊工况;
我分享一篇好的论文:
Wide-Range ZVS Control Technique forBidirectional Dual-Bridge Series-Resonant DC–DC Converters
文献的拓扑虽然不是基于双有源桥的SRDAB,但是后续作者分析了控制算法对不同拓扑的适用性,提出了统一的控制算法。
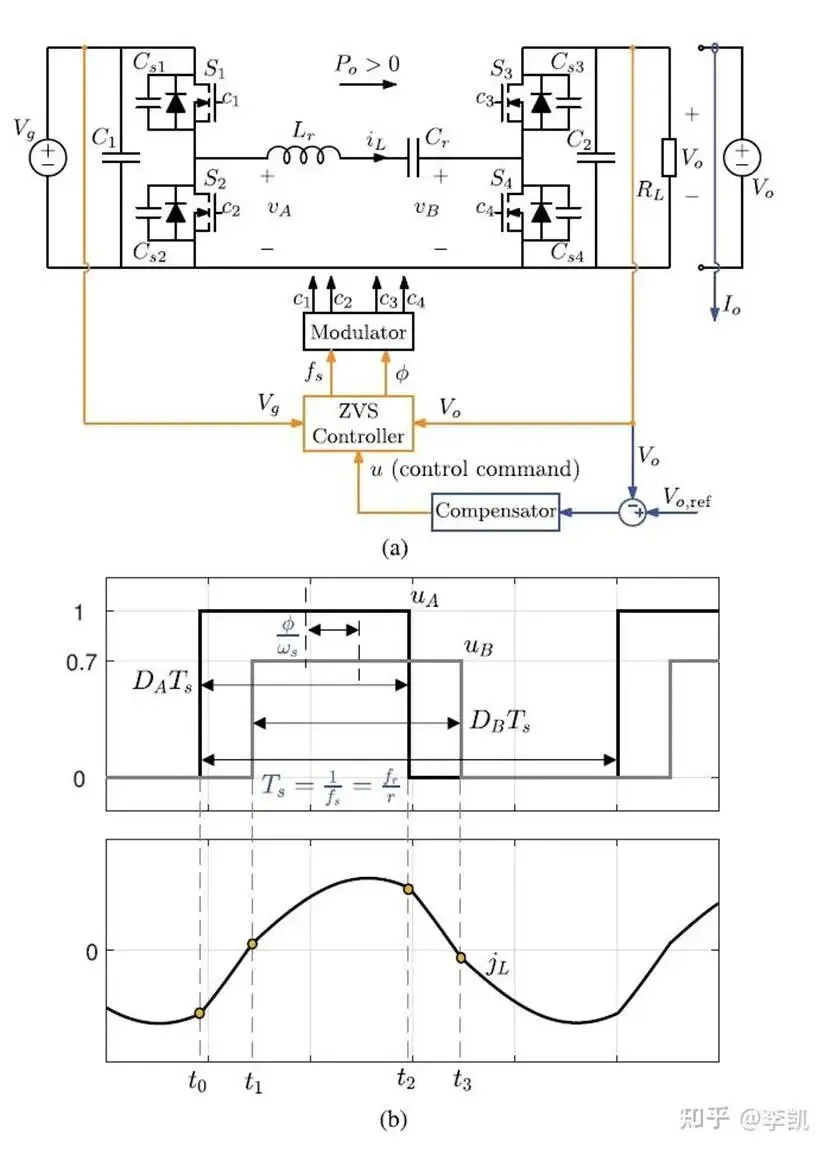
文章的本质是基于SRDAB的谐振电感和谐振电容列出状态方程,基于上述4个时刻,把软开关的条件作为限定,求解出来需要满足的相位角,相位角又和开关频率相关,因此可以首先通过环路计算得到开关频率,然后通过状态方程的解析解得到移相角;
具体的计算过程和控制框图如下图:

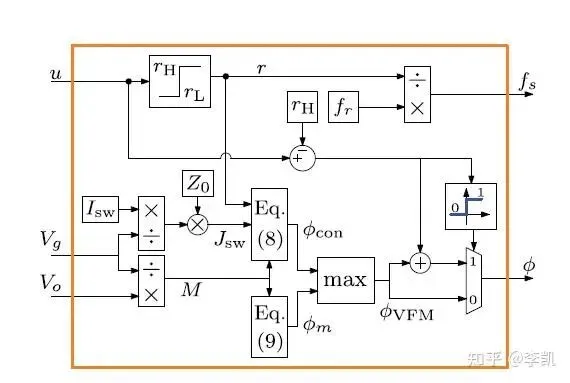
上图的Eq.8和Eq.9写错了,应该是Eq.12和Eq.13;
下面是仿真效果;
Boost升压模式,输入电压100V, 输出电压150V:
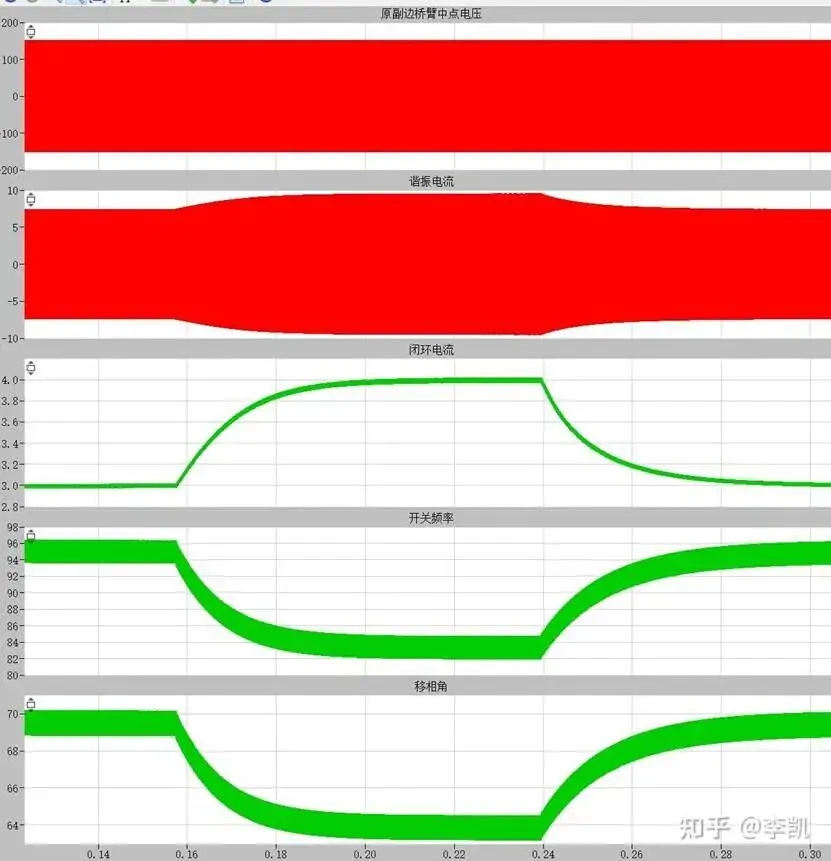
开关频率96k切换到84K,然后恢复到96k
动态闭环,增减载3A和4A负载切换能闭环,动态调节开关频率和移相角;
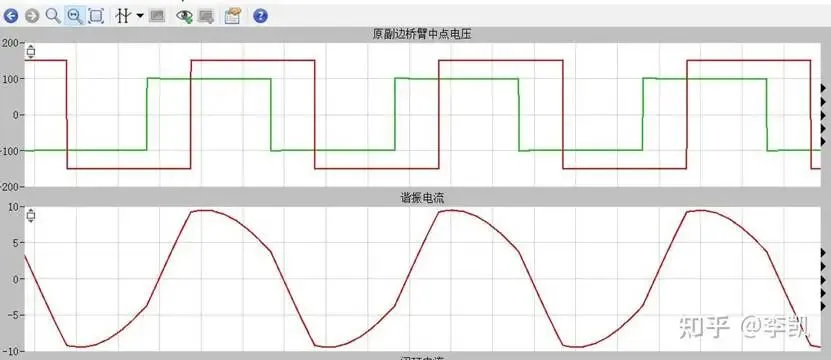
谐振腔感性电流实现ZVS
谐振电流滞后桥臂中点电压,感性电流实现软开关;
Buck降压模式,输入电压150V, 输出电压100V:
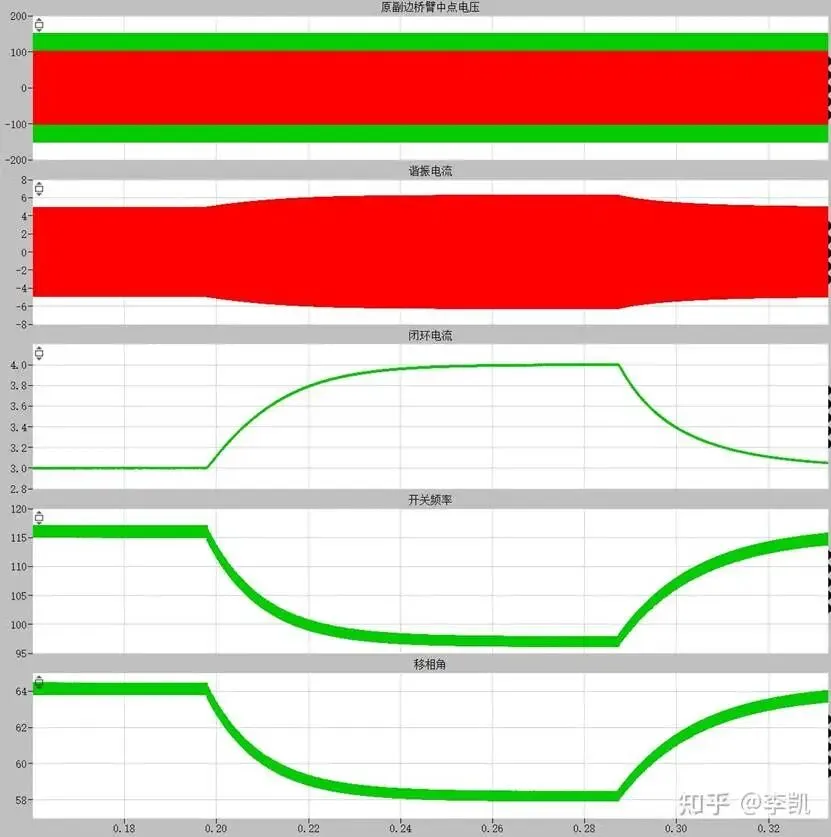
开关频率115k切换到96k, 然后恢复
动态闭环,增减载3A和4A负载切换能闭环,动态调节开关频率和移相角;
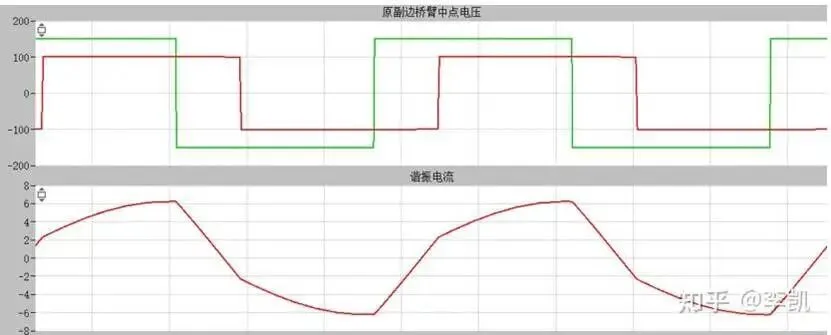
感性电流实现ZVS
谐振电流滞后桥臂中点电压,感性电流实现软开关;
文献还详细描述了增益和输出功率的关系,提出了如果开关频率调节到了限值,应该保持开关频率不变继续调节移相角的PSM控制算法;
后续我会继续分析PSM;