CUDA学习笔记:如何通过提升计算强度来优化矩阵乘法(一)
- 2026-02-08 23:05:52
1. 写在前面
咱们接着之前的CUDA学习笔记系列,继续深入优化矩阵乘法的性能。简单回顾一下,在之前的内容中,我们以 naive 矩阵乘法为基础,先后通过紧凑全局内存访问、共享内存等核心技术,逐步提升了矩阵乘法的运算效率。
在 RTX 5060Ti 显卡上对4096×4096大小的矩阵进行测试,最佳性能已达到 1855.5 GFLOPS(FLOPS,即Floating-Point Operations Per Second,每秒浮点运算次数)。今天,我们就在这个基础上,继续优化,争取让性能再上一个台阶。
回顾我们之前实现的 kernel 函数,会发现一个共性特点:一个线程仅负责计算一个输出数据。这种方式会导致全局显存与共享显存的利用率偏低——数据加载后未能充分复用,访存效率受限。由此我们思考:能否让一个线程负责计算多个输出数据?这样一来,输入数据加载到共享显存后可被多次利用,访存利用率会显著提升,而矩阵计算的计算强度(可简单理解为计算量与内存访问量的比值)也会随之提高。
本篇博客围绕这一思路,在共享内存优化基础上,通过1D-tiling(分块)实现单线程计算多个结果,进一步挖掘性能潜力。接下来我们来看具体实现方法和kernel实现。
2. 基于1D-tiling(分块)实现单线程多元素计算
这个kernel(我们称为kernel4)的实现流程和思路与上一个基于共享内存优化的kernel类似,但在之前的基础上,增加了一个新的内层循环,用于在一个线程中计算多个结果矩阵C中的数据。下图是kernel计算过程的可视化,橙色和红色部分分别表示两个线程在内层循环中的数据访问情况。
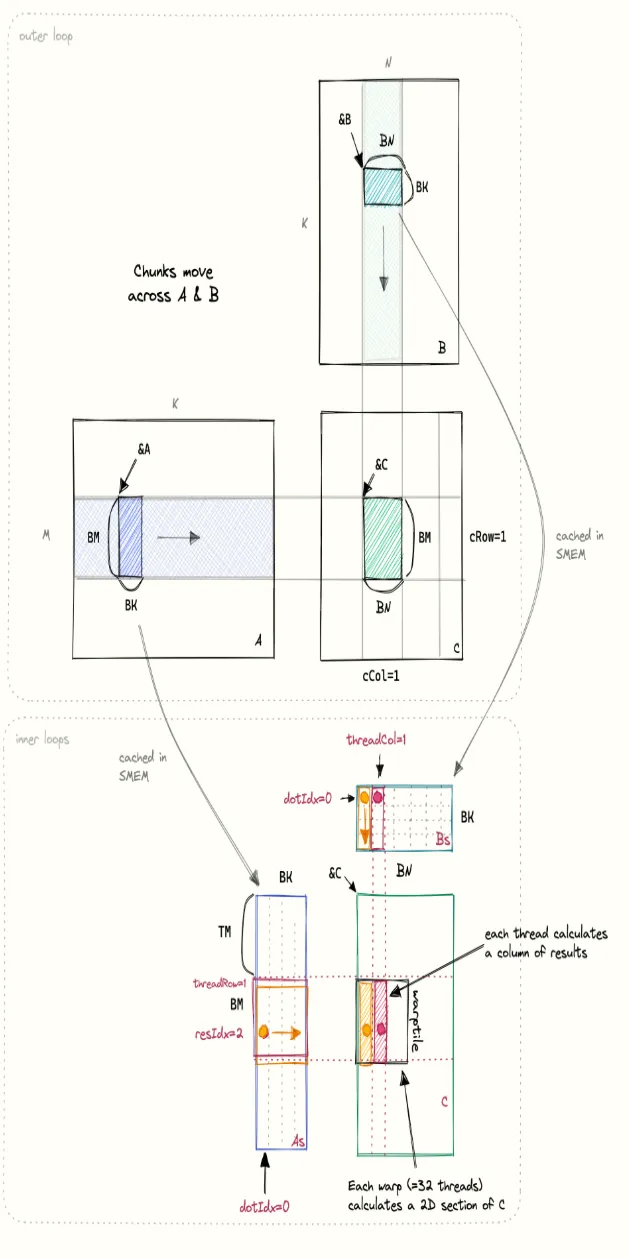
这里我想先对这个图做一个细致的解释,这对理解接下来的所有内容至关重要。
首先,图片上面C矩阵中浅绿色部分BMxBN大小的矩阵是由A矩阵中紫色的行条带和B矩阵中浅绿色的列条带计算得到,但这个计算过程不是一次完成的,而是通过矩阵A中BMxBK的矩阵块(chunk)和矩阵B中BKxBN的矩阵块在行、列条带上滑动相乘并相加得到,每次滑动的距离都是BK,分别对应A矩阵块的列宽和B矩阵块的行高。上面介绍的都是外层循环的内容。
下面的图描述的则是内层循环的过程,这时A、B矩阵中的矩阵块分别已经加载进共享显存As和Bs中,这篇博客的重点就是怎么加速这部分的计算。内层循环这里画了两个线程,我们先来看黄色部分的线程,图中每个原点表示一个数据,dotIdx从0到BK,表示As矩阵块中的一列元素向右移动,Bs矩阵块中的一行元素向下移动。这个kernel提高访存利用率的关键就在于Bs中的一个元素会被重复使用TM次,分别与As中高为TM的一列元素相乘,所以左下图中As中黄色和红色矩形框的高度都是TM。而每个线程则负责计算C中一个高度为TM的列,如内层循环中右下图所示,黄色和红色两个线程分别负责计算C矩阵中两个相邻的高度为TM的列,一个线程束(32个线程)则负责计算矩阵C中TMx32的矩形区域。
和上一个kernel相比,这个kernel所有的重要变化都发生在内层循环中,全局内存到共享内存的加载等过程基本保持不变,下面让我们来看看kernel中内层循环的实现:
float threadResults[TM] = {0.0};// 外层循环:在条带上移动,来实现完整的计算for (uint bkIdx = 0; bkIdx < K; bkIdx += BK) {// 将图中A矩阵中的大小为BMxBK大小的矩阵块加载到共享内存As中// 将图中B矩阵中的大小为BKxBN大小的矩阵块加载到共享内存Bs中// 加载完后,A矩阵和B矩阵的数据地址位置会分别在行条和列条上发生移动As[innerRowA * BK + innerColA] = A[innerRowA * K + innerColA];Bs[innerRowB * BN + innerColB] = B[innerRowB * N + innerColB];__syncthreads();// 由于数据在内存中是按照行优先的顺序通过一维方式进行线性存储的// 所以每算完条带上的一个矩阵块,A、B矩阵块的起始位置就要进行移动A += BK;B += BK * N;// 当前线程的计算部分for (uint dotIdx = 0; dotIdx < BK; ++dotIdx) {// As矩阵块中的一列元素向右移动,Bs矩阵块中的一行元素向下移动// 定位到Bs矩阵中特定的元素,在内存循环的计算中被复用float tmpB = Bs[dotIdx * BN + threadCol];for (uint resIdx = 0; resIdx < TM; ++resIdx) {// TM在这里表示一个线程负责计算的元素的数量,也是As中向右移动的一列元素的高度,// resIdx表示在这一列元素中的位置threadResults[resIdx] +=As[(threadRow * TM + resIdx) * BK + dotIdx] * tmpB;}}__syncthreads();}
关于As[(threadRow * TM + resIdx) * BK + dotIdx]的索引,可能很多人看到这里不是很理解,这里我们做一下说明,理解这个索引也是理解1D block tiling的关键。
首先,说明以下,根据theradRow的计算方式:
const int threadCol = threadIdx.x % BN;const int threadRow = threadIdx.x / BN;
threadRow 是把所有线程按 BN 个一组进行分组后的组号,而不是直接对应 C 子块中的行号。那么为什么要乘TM呢?因为每个线程负责计算 C 子块中连续 TM 行的结果(在同一列上)。我们在后面看C矩阵索引的时候会通过图示进一步说明,这里先有一个大致的印象即可。
Kernel 4的完整内容如下:
#pragma once#include<algorithm>#include<cassert>#include<cstdio>#include<cstdlib>#include<cublas_v2.h>#include<cuda_runtime.h>#define CEIL_DIV(M, N) (((M) + (N)-1) / (N))template <const int BM, const int BN, const int BK, const int TM>__global__ voidsgemm1DBlocktiling(int M, int N, int K, float alpha,const float *A, const float *B, float beta,float *C) {const uint cRow = blockIdx.y;const uint cCol = blockIdx.x;// 每个 warp 会计算 32*TM 个元素, 线程的这种一维布局方式有利于全局内存合并访问const int threadCol = threadIdx.x % BN;const int threadRow = threadIdx.x / BN;// 为当前 blocktile 分配共享显存// 每个 blocktile 负责A中BMxBK大小的矩阵和B中BKxBN大小矩阵块的计算__shared__ float As[BM * BK];__shared__ float Bs[BK * BN];// 当前线程负责计算的 blocktile 在A矩阵和B矩阵中的位置A += cRow * BM * K; // A行条起始的位置(行条最左边的位置)B += cCol * BN; // B列条起始的位置(列条最上面的位置)C += cRow * BM * N + cCol * BN; // C矩阵在A行条、B列条起始位置时的位置(行优先)assert(BM * BK == blockDim.x);assert(BN * BK == blockDim.x);const uint innerColA = threadIdx.x % BK; // warp-level GMEM coalescingconst uint innerRowA = threadIdx.x / BK;const uint innerColB = threadIdx.x % BN; // warp-level GMEM coalescingconst uint innerRowB = threadIdx.x / BN;// allocate thread-local cache for results in registerfilefloat threadResults[TM] = {0.0};// 三层循环进行计算,上面已经解释过了...// 将计算结果写回C矩阵// 每个线程计算TM个C的部分结果,多次在A行条和B列条滑动矩阵乘法结果的累加// 等效性在前面的文章做过论述,本质上是两个长向量乘法求和拆分成多个短向量乘法求和再相加for (uint resIdx = 0; resIdx < TM; ++resIdx) {C[(threadRow * TM + resIdx) * N + threadCol] =alpha * threadResults[resIdx] +beta * C[(threadRow * TM + resIdx) * N + threadCol];}}
关于C[(threadRow * TM + resIdx) * N + threadCol]这里的索引,我们做一下详细的解释。
1D tiling的详细过程如下所示:

T(r,c) 表示 threadRow=r, threadCol=c 的线程负责计算。
以 threadRow=1, threadCol=2 的线程为例,它负责的是:
C[4][2], C[5][2], C[6][2], C[7][2] (TM=4 时)↑ 行方向有 TM 个 ↑ 列方向只有 1 个
对应图中的标红红并加深的部分。
所以:
行方向:每个线程负责 TM 行 → 需要 threadRow * TM + resIdx 来定位
列方向:每个线程只负责 1 列 → threadCol 直接就是列号,不需要乘任何东西
但如果是 2D Block Tiling,每个线程会在行和列两个方向都负责多个元素,这时两个方向就都需要乘 tiling 的系数,这部分内容我们后续会继续学习并解读。
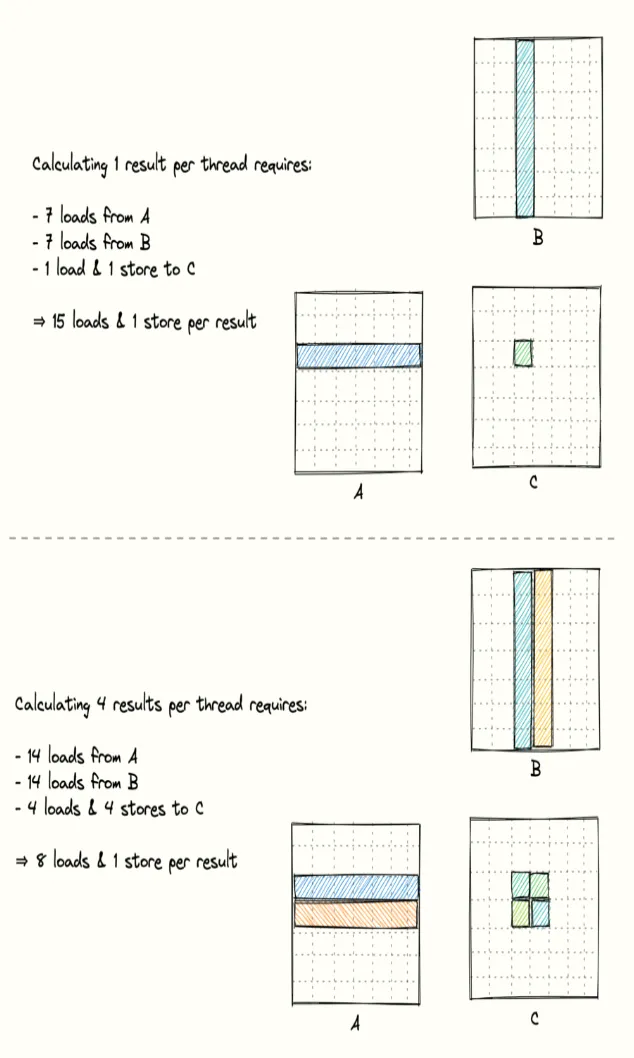
最后,我们通过一个简单的图示和计算来更直观看看如何通过数据复用来提升计算强度:
3. 总结
本篇博客中,我们在之前kernel实现的基础上,提出了通过提升访存利用率来增强计算强度的优化思路。具体实现上,我们采用单线程负责计算矩阵C中多个元素的方式,结合1D block tiling技术,实现了对Bs中元素的重复利用,有效减少了Bs元素的访问次数,最终显著提升了计算强度。
测试结果显示,kernel4在4096×4096大小的矩阵测试中(RTX 5060Ti),性能达到5760.8 GFLOPS,相比此前kernel3的性能提升了2.11倍。
在后续的系列文章中,我们将继续解读如何通过2D block tiling技术进一步提升计算强度,实现kernel性能的再突破。
4. 参考
https://siboehm.com/articles/22/CUDA-MMM
https://github.com/siboehm/SGEMM_CUDA/tree/master
