2D 线弹性:从强形式到弱形式
这篇我们可以将第一篇中 1D 结构强形式与弱形式的推导思路搬过来。可以理解为把原来的一根 杆 的拉伸扩展为一块 薄板 的拉伸,即未知量从一个位移 扩展为两个位移分量 。
1. 微积分回顾
很多教材一会儿写成向量箭头,一会儿写成矩阵粗体,很容易被符号绕晕。因此我们先约定:
- • 粗体 : 列向量/矩阵表示,更偏向计算或代码实现。
1.1 向量
假设沿着 和 的单位向量分别表示为 和 ,那么二维向量表示为:
点积(scalar product):
梯度算子(Gradient):
对标量场 :
散度(Divergence)将向量场压成标量:
1.2 矩阵
把同一个向量写成列向量:
点积变成矩阵乘法:
梯度算子写成列向量:
对标量场 :
散度(Divergence):
1.3 一个关键公式
与 1D 中的分部积分类似,我们最需要的其实就一个公式:
把 这种体积分转换为边界上的积分 + 另一个体积分。
我们从一个非常常见的乘积求导开始:
对整个区域 积分:
再用散度定理(把左边体积分变成边界积分):
将 Eq.13 代入 Eq.12 并整理即可得 格林公式(Green’s formula):
格林定理(Green’s theorem)
散度定理(Divergence theorem)
2. 强形式
先明确未知量:二维位移场(两个分量)
线弹性常见假设:
2.1 几何方程
下图表示 应变 本质上就是 位移在空间里的变化率。
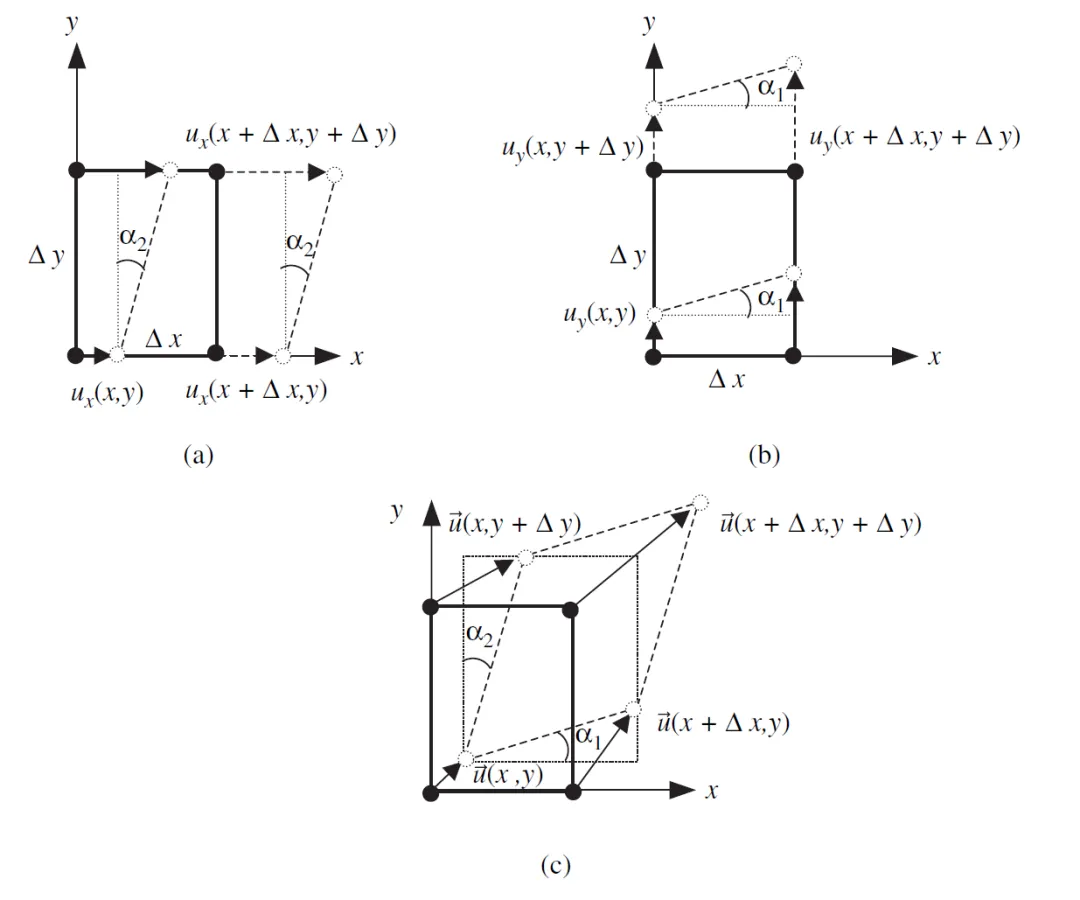
(a) 纯 方向拉伸:
(b) 纯 方向拉伸:
(c)剪切变形:上边相对下边发生水平滑移,同时右边相对左边发生竖直滑移。因此剪切变形同时包含 随 的变化和 随 的变化:
将其写为矩阵形式有:
其中
2.2 物理方程
在 2D 中,应力可以理解为:作用在某个切面上的单位面积力(traction)。
我们考虑两类最常见的切面:法向分别沿 和 方向的切面。
其中 :第一个下标 表示切面法向方向;第二个下标 表示力的方向。
例如 表示:法向为 的切面上,沿 方向的剪应力。
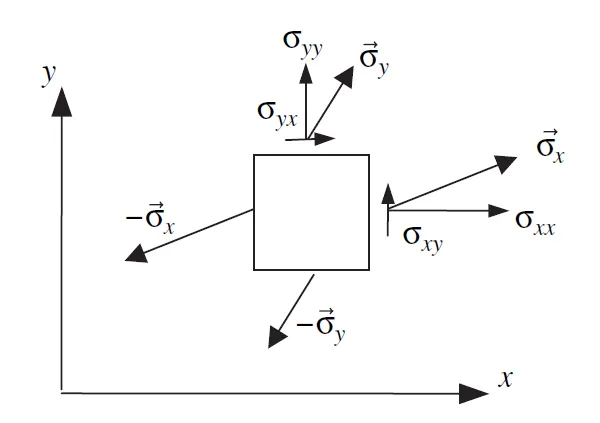
由微元力矩平衡可得剪应力对称:
因此,应力可写成列矩阵:
或者 对称矩阵:
线弹性本构关系(胡克定律的 2D 形式)写作:
其中 取决于平面应力/平面应变假设。
2.3 平衡方程
(1)整体
如下图(a)所示,我们考虑一个任意形状,单位厚度的二维区域 ,边界为 。 外力主要来自于:
- • 体力(body force):分布在区域内部,单位体积的力(二维里可理解为单位面积×单位厚度)。如重力,磁力等。
- • 边界牵引(surface traction):分布在边界上,每单位面积的力(二维里就是每单位长度×单位厚度)牵引力的方向由边界处的外法向 决定。
(2)局部微元
如下图(b)所示,在点 周围取一个矩形微元,边长分别为 和 。我们用之前定义的应力向量:
因此:
同理,上下边界分别给出作用力,再加上体力 作用在微元体积(面积×厚度) 上。
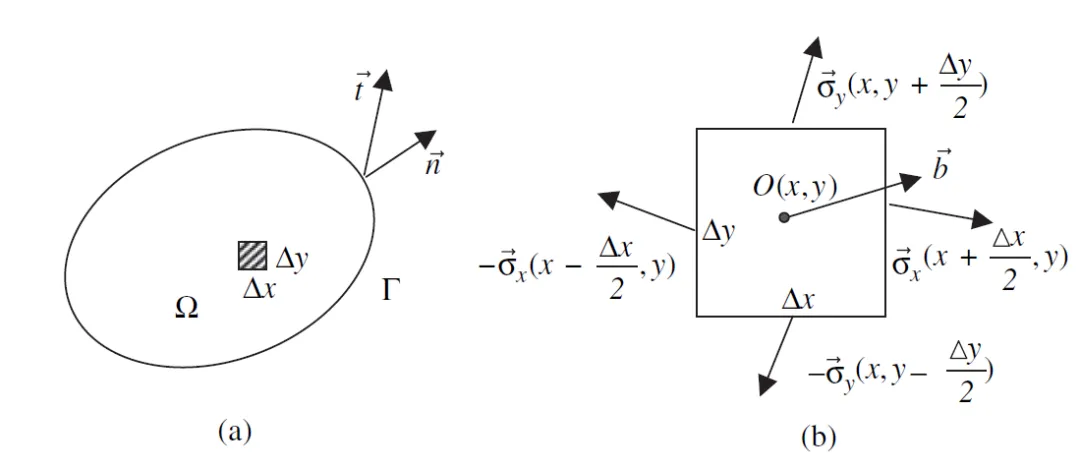
(3)微元的静力平衡
把四条边的牵引力与体力全部加起来,静力问题要求合力为零:
(4)局部微分形式
将 Eq.23 两边同时除以 得:
当 且 时,括号里的差商就变成偏导数:
这就是 2D 线弹性(静力)最核心的平衡方程。
(5)分量与矩阵形式
将 Eq.25 两边分别乘 和 得两条标量方程:
写成矩阵形式:
其中
2.4 Cauchy 牵引定理
前面我们已经引入了两个应力向量,分别记为 和 。Cauchy 牵引定理 想告诉我们的是:在同一点处,只要知道 和 ,就能得到该点处任意方向切面上的牵引力
(1)任意切面 + 一个三角微元
如下图所示,取一个三角微元:
- • 斜边是我们关心的任意方向切面,长度为 ,外法向为单位向量
- • 另外两条直角边分别与坐标轴垂直,对应长度为 与
法向 可以写成分量形式:
图中斜边是任意切面,其上的牵引力(面力密度)记为 。同时,在两个坐标面上,牵引向量分别为 和 。
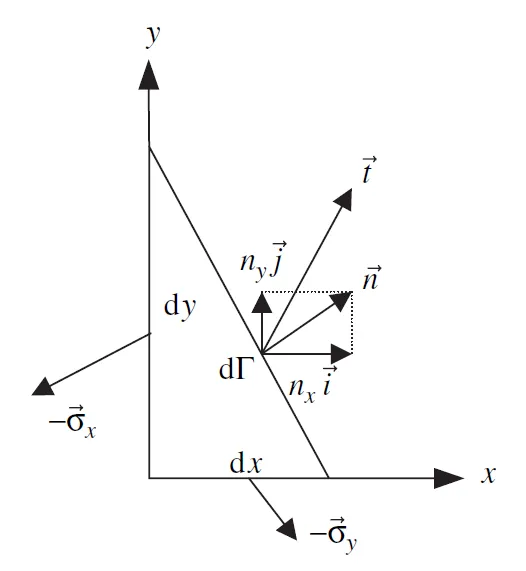
(2)三角微元力平衡
不考虑惯性项,三条边上的合力为零:
两边除以 并且注意有 和 ,则我们可得:
其物理意义是:任意切面上的牵引 ,就是把 和 按照法向分量 和 做线性组合。
(3) 分量与矩阵形式
Eq.30 两边分别乘以 和 有
Eq.31 写成矩阵形式,就是经典的 Cauchy 牵引定理:
含义为:给定某点的应力张量 ,再给定该点处任意单位法向 ,就能得到该取向切面上的牵引力(面力密度)。
2.5 边界条件
与 1D 类似,边界条件也分两类:
- • 牵引边界(traction or natural or Neumann)
- • 位移边界(displacement or essential or Dirichlet)
并且满足
2.6 强形式小结
总结来说,2D 线弹性的强形式为:
3. 弱形式
强形式中有 以及 ,这意味着强形式最终会要求 至少能做二阶导。弱形式的目标是只让 需要一阶导就够用。
3.1 从平衡方程出发:乘权函数并积分
我们分别对两条平衡方程(, 两个方向)乘上权函数并积分;同时把牵引边界条件写成“加权残量为零”的形式,方便后面直接代入。
3.2 用格林公式:把导数从 上挪到 上
用格林公式 Eq.14 可得:
两式相加,并结合 Eq.36 (a) 和 (b) 可得:
3.3 考虑边界条件
在位移边界条件 上,位移已被固定(本质边界条件)。为了不在 上引入额外未知量,则 和 在 上应为 0,因此边界积分 那部分自动消失,只剩下牵引边界 。同时利用 Cauchy 牵引定理,即 Eq.36 (c)和(d),Eq.38 可整理为:
Eq.39 左边被积项展开有:
最后代入本构 ,得到弱形式:
4. 举例:薄板单向拉伸
4.1 问题描述
如下图所示,有一薄板,设板域 ,平面应力。
- • 为了去掉刚体平移(竖向整体漂移),在左下角加一个点约束:
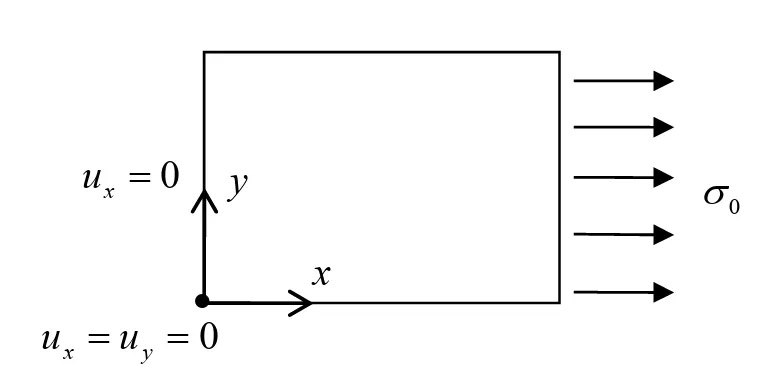
4.2 强形式
本例无体力,则强形式可写为:
其中
边界条件为
4.3 精确解
右端施加的是均匀拉应力,而且没有体力,因此板内只有 。再根据本构关系可推得应变,进一步可反推得位移。
4.4 弱形式
在该例中,无体力 ,则弱形式写作:
右端只有 那条边有力:
(1) 选一个试函数
因为我们预期解是线性的,我们就直接用两参数线性位移场:
它自动满足 , 且
取同类权函数:
其中 , 是任意常数。
(2) 计算应变、应力
位移的应变:
平面应力由本构得:
对权函数求偏导:
(3) 代入弱形式
弱形式左端:
右端:
左右相等:
因为 , 是任意的,所以
(4) 求解 ,
由
第二式给
代回一式:
因此
最终
参考文献
- • Fish, Jacob, and Ted Belytschko. A First Course in Finite Elements. Wiley, 2007.