n
第2课时 事件的相互独立性(二)
[学习目标] 1.掌握事件相互独立的定义,及其与对立事件的区别.(重点)2.会利用相互独立事件概率公式求比较复杂的概率问题.(难点)
导语
前面我们学习了事件的相互独立性,事件A与事件B相互独立是如何定义的呢?两事件独立,与它们的对立事件又有什么关系呢?
一、相互独立事件的有关证明
例1若P(A)>0,P(B)>0,证明:事件A,B相互独立与A,B互斥不能同时成立.
证明若事件A,B相互独立,
则P(AB)=P(A)P(B)>0;
若事件A,B互斥,则P(AB)=0,
所以当P(A)>0,P(B)>0时,事件A,B相互独立与A,B互斥不能同时成立.
反思感悟利用两个事件相互独立和互斥的定义证明了在两个事件的概率不为0的情况下,互斥和相互独立不能同时成立,也就是说如果两个事件的概率不是0并且互斥的情况下,这两个事件就不独立.
跟踪训练1 证明必然事件Ω和不可能事件∅与任意事件相互独立.
证明设任意事件记作A,
则A∩Ω=A,A∩∅=∅.
因为P(Ω)=1,P(∅)=0,
所以P(AΩ)=P(A)=P(A)×1
=P(A)P(Ω),
P(A∅)=P(∅)=0=P(A)×0=P(A)P(∅),
所以A与Ω,A与∅都相互独立.
二、相互独立事件概率的计算
例2甲、乙、丙三人分别独立解一道题,甲做对的概率是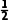 ,三人都做对的概率是
,三人都做对的概率是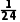 ,三人全做错的概率是
,三人全做错的概率是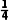 .
.
(1)分别求乙、丙两人各自做对这道题的概率;
(2)求甲、乙、丙中恰有一个人做对这道题的概率.
解(1)分别设“甲、乙、丙三人各自做对这道题”为事件A,B,C,
则P(A)=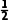 ,由题意得
,由题意得
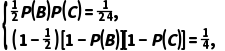
解得P(B)=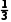 (C)=
(C)=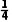 或P(B)=
或P(B)=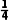
P(C)=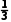 .
.
所以乙、丙两人各自做对这道题的概率分别为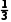 和
和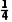 或
或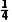 和
和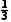 .
.
(2)设“甲、乙、丙三人中恰有一人做对这道题”为事件D,
则P(D)=P(A)P(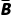 )P(
)P(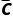 )+P(
)+P(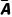 )P(B)P(
)P(B)P(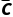 )+P(
)+P(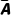 )P(
)P(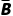 )P(C)=
)P(C)=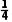 +
+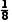 +
+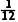 =
=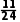 .所以甲、乙、丙三人中恰有一人做对这道题的概率为
.所以甲、乙、丙三人中恰有一人做对这道题的概率为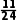 .
.
反思感悟求解相互独立事件的概率的具体步骤
(1)确定各事件是否相互独立.
(2)确定各事件是否会同时发生.
(3)先确定每个事件的概率,再计算其积.
跟踪训练2一次数学考试的试卷上有4道填空题,共20分,每道题完全答对得5分,否则得0分,在试卷命题时,设计第一道题使考生都能完全答对,后三道题能得出正确答案的概率分别为p,,,且每题答对与否相互独立.
(1)当p=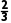 时,求考生填空题得满分的概率;
时,求考生填空题得满分的概率;
(2)若考生填空题得10分与得15分的概率相等,求p的值.
解设“考生填空题得满分、15分、10分”分别为事件A,B,C.
(1)P(A)=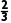 ×
×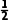 ×
×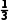 =
=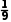 .
.
(2)P(B)=p×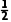 ×
×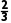 +p×
+p×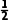 ×
×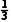 +(1-p)×
+(1-p)×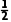 ×
×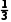 =
=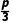 +
+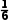
P(C)=p×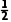 ×
×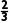 +(1-p)×
+(1-p)×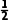 ×
×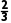 +(1-p)×
+(1-p)×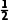 ×
×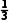 =
=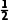 -
-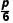
因为P(B)=P(C),所以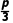 +
+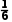 =
=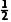 -
-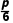
解得p=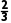 .
.
三、相互独立事件的综合应用
例3有甲、乙、丙三支足球队互相进行比赛,每场都要分出胜负,已知甲队胜乙队的概率是0.4,甲队胜丙队的概率是0.3,乙队胜丙队的概率是0.5,现规定比赛顺序:第一场甲队对乙队,第二场是第一场中的胜者对丙队,第三场是第二场中的胜者对第一场中的败者,以后每一场都是上一场中的胜者对前一场中的败者,若某队连胜四场则比赛结束,求:
(1)第四场结束比赛的概率;
(2)第五场结束比赛的概率.
解(1)因为甲连胜四场的概率P1=0.4×0.3×0.4×0.3=0.0144.
乙连胜四场的概率P2=0.6×0.5×0.6×0.5=0.09,
所以第四场结束比赛的概率P=P1+P2=0.0144+0.09=0.1044.
(2)第五场结束比赛即某队从第二场起连胜四场,只有丙队有可能.
若甲胜第一场,则丙连胜四场的概率P3=0.4×0.7×0.5×0.7×0.5=0.049,
若乙胜第一场,则丙连胜四场的概率P4=0.6×0.5×0.7×0.5×0.7=0.0735,所以第五场结束比赛的概率P5=P3+P4=0.1225.
反思感悟求较复杂事件的概率的一般步骤
(1)列出题中涉及的各个事件,并且用适当的符号表示.
(2)理清事件之间的关系(两个事件是互斥还是对立,或者是相互独立的),列出关系式.
(3)根据事件之间的关系准确选取概率公式进行计算.
(4)当直接计算符合条件的事件的概率较复杂时,可先间接地计算其对立事件的概率,再求出符合条件的事件的概率.
跟踪训练3某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,假设甲队每人回答问题的正确率均为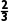 ,乙队每人回答问题的正确率分别为
,乙队每人回答问题的正确率分别为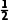 ,且两队每人回答问题正确与否相互之间没有影响.
,且两队每人回答问题正确与否相互之间没有影响.
(1)求甲队总得分为3分的概率;
(2)求甲队总得分为3分且乙队总得分为1分的概率.
解(1)记“甲队总得分为3分”为事件A,
甲队得3分,即三人都回答正确,
其概率P(A)=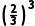 =
=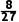 .
.
(2)记“乙队总得分为1分”为事件B.
乙队得1分,即乙队三人中只有1人回答正确,其余2人回答错误,
则P(B)=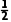 ×
×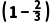 ×
×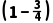 +
+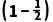 ×
×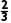 ×
×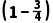 +
+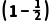 ×
×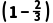 ×
×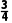 =
=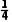
由题意得事件A与事件B相互独立,
则甲队总得分为3分且乙队总得分为1分的概率为P(AB)=P(A)P(B)=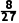 ×
×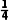 =
=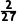 .
.
1.知识清单:
(1)相互独立事件的证明.
(2)相互独立事件概率的计算.
(3)相互独立事件的综合应用.
2.方法归纳:构造方程(组)、正难则反思想求概率.
3.常见误区:相互独立事件与互斥事件易混淆.
1.一个电路上装有甲、乙两根保险丝,甲熔断的概率为0.85,乙熔断的概率为0.74,甲、乙两根保险丝熔断与否相互独立,则两根保险丝都熔断的概率为( )
A.1B.0.629
C.0D.0.74或0.85
答案 B
解析设“甲保险丝熔断”为事件A,“乙保险丝熔断”为事件B,
则P(A)=0.85,P(B)=0.74,
由事件A与B相互独立,
得“两根保险丝都熔断”为事件AB,
∴P(AB)=P(A)·P(B)=0.85×0.74
=0.629.
2.已知一批学生体形合格的概率为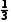 ,视力合格的概率为
,视力合格的概率为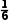 ,其他综合标准合格的概率为
,其他综合标准合格的概率为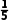 ,从中任选一学生,则三项均合格的概率为(假设三项标准互不影响)( )
,从中任选一学生,则三项均合格的概率为(假设三项标准互不影响)( )
A.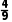 B.
B.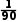
C.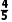 D.
D.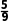
答案 B
解析由题意知三项标准互不影响,
∴P=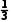 ×
×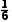 ×
×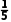 =
=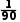 .
.
3.已知甲、乙、丙3名运动员击中目标的概率分别为0.7,0.8,0.85,且3人是否击中目标相互独立.若他们3人向目标各发1枪,则目标没有被击中的概率为.
答案 0.009
解析 3人向目标各发1枪,由相互独立事件的概率计算公式,得目标没有被击中的概率P=(1-0.7)×(1-0.8)×(1-0.85)=0.3×0.2×0.15=0.009.
4.假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一个准时响的概率是.
答案 0.98
解析至少有一个准时响的概率为1-(1-0.90)×(1-0.80)=1-0.10×0.20=0.98.
课时对点练 [分值:100分]
单选题每小题5分,共30分;多选题每小题6分,共24分

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享