本期会拆解CHAPTER H 的内容
单向或者双向受轴力/是否受到扭转的组合作用/或者只受到扭转作用
(组合构件详见章节CHAPTER I)
本章节共分为H1~H4

| H1: 受到轴向力和弯曲同时作用的单向和双向截面对称的构件 H2: 非对称和其他构件在弯曲和轴向力作用下的设计 H3: 受到扭转或组合作用(扭转、弯曲、剪力、轴向力)的构件 H4: 带螺栓孔的翼缘在拉伸作用下的断裂 |
ØH1: 受到轴向力和弯曲同时作用的单向和双向截面对称的构件
H1.1同时受到压弯的单向或双向截面对称的构件,是指受到压弯应力的双向对称构件和一个方向的几何轴被限制的单对称截面,这种情况下的构件不需要考虑复杂的双向弯曲相互作用,常见的单向截面对称如槽钢、T型钢等,常见的双向截面对称构件如H型钢。H1-1a和H1-1b给出了压弯构件的相互作用强度限制要求,以轴向力的作用力程度区分,要求当轴向力较大时,需要更严格的控制(H1-1b)。
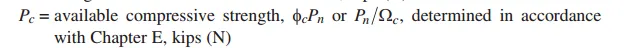
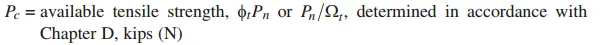
H1.2同时受到拉弯作用的单向或双向对称截面的构件,这一小篇章虽然是受到拉弯作用,但是与压弯作用使用一样的H1-1a和H1-1b,但是的区别在于其中的Pc,压弯构件的Pc取章节E中,拉弯构件Pc取章节D。其实从这一章开始,多了和之前DEF章节的联动,很多都是在不同类型的受力同时产生的时候,补充了很多需要系数的复核计算。

H1.3同时受到单轴压弯作用的双向热轧截面,这其实是H1.1的特殊情况,即侧向无支撑长度要小于y向弯曲屈曲有效长度,感觉很拗口,首先要明确这里的x,y其实强轴和弱轴的概念,限制Lcz≤Lcy的实际意义其实就是限制构件的扭转屈曲先于弯曲屈曲,而y轴的屈曲荷载较小,所以限制y轴是保守设计的体现。当满足这个条件时,可以从instability in-plane和buckling out-of-plane进行区别简化,适当简化考虑组合力的作用,平面内不稳定仍然使用H1-1a/b,平面外屈曲可以使用公式H1-3。
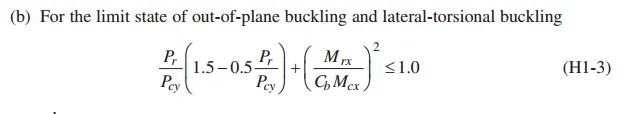
文字过于繁琐,简单来看,这一章节H1的逻辑就是,一般的压弯作用截面设计使用H1.1的内容,拉弯作用截面看H1.2,特殊情况的压弯平面外复核简化方法看H1.3。
ØH2: 受到轴向力和弯曲同时作用的非对称截面
H2的标题很繁琐,其实简单来说,就是H1没考虑的截面类型就看H2,H2也可以完全替代H1计算所有截面,H1其实也就是H2的特殊情况和简化计算。
ØH3: 受到扭转或组合作用(扭转、弯曲、剪力、轴向力)的构件
H3从标题就透露着不一般,因为它涵盖了太多作用组合,既包括只受扭转作用的构件,也包括存在组合作用(扭转、弯曲、剪力、压力、拉力组合作用)的情况。
H3.1仅受扭转作用的圆形和矩形HSS,与其他作用一样,篇章先两种设计方法分别对应的扭转强度Tn:
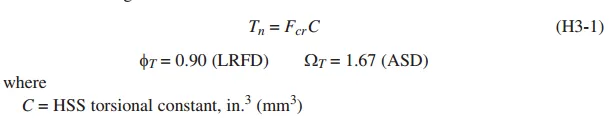
其中临界应力Fcr的公式详见H3-2(round HSS);rectangular HSS的临界应力详见公式H3-3~H3-5。
H3.2受组合作用的HSS,因为组合作用很复杂,所以AISC给出了简化计算,当所需扭转强度Tr(the required torsional strength)小于20%的可用扭转强度Tc(the available torsional strength),可以忽略扭转效应,按H1计算。

当超过20%,则不能忽略扭转效应,需要考虑组合作用的的相互作用,详见公式H3-6。
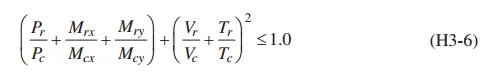
H3.3受扭转和组合作用的非HSS构件,the available torsional strength取正应力屈服(yielding under normal stress)、剪切屈服(shear yielding under shear stress)、屈曲(buckling)的最小值,确保了构件在这三种可能得破坏模式下都有足够的安全储备能力。

ØH4: 带螺栓孔的翼缘在拉伸作用下的断裂
本节是针对受拉翼缘存在螺栓孔的构件,同时承受着轴向拉力和强轴弯曲作用共同作用下产生的拉应力,翼缘的断裂强度限值为公式H4-1,这个公式确保了在螺栓孔附近应力集中的区域,这个构件不会发生拉伸断裂破坏。

本期内容主要就是CHAPTER H,这个章节内容不多,大家同样可以静下心来详细阅读一遍,有遗漏或者错漏的大家可以留言,或者加入交流群一起探索。其他章节往下点合集看~
