第二章 谓词演算(详细解析)
第二章是《人工智能:复杂问题求解的结构和策略》技术内容的核心开篇,承接第一章提出的“形式逻辑是AI符号推理基础”的观点,聚焦"谓词演算"这一AI核心表示语言。本章通过系统讲解谓词演算的语法、语义、推理规则及应用,回答“如何用形式化语言精准描述知识”“如何基于语言进行逻辑推理”两大问题,为后续状态空间搜索、专家系统等技术提供核心工具,是AI符号主义路线的基石章节。
核心逻辑脉络:从基础的命题演算切入(铺垫)→ 引出谓词演算的必要性(解决命题演算的局限性)→ 拆解谓词演算的语法与语义(精准建模知识)→ 掌握核心推理规则(实现逻辑推导)→ 结合实例与应用(落地到AI问题求解)。
一、命题演算:谓词演算的基础铺垫
命题演算是最简单的形式逻辑系统,主要处理“命题”(能判断真假的陈述句)及命题间的逻辑运算,是谓词演算的简化版本,先掌握其核心规则,可快速过渡到复杂的谓词演算。
1.1 命题的定义与表示
命题是具有明确真值(真/假,用1/0表示)的陈述句,不能同时为真又为假,也不能是疑问句、祈使句。
1.2 命题演算的逻辑联结词(与第一章布尔代数对应)
命题演算的联结词与布尔代数运算完全对应,是逻辑推理的核心工具,具体如下表所示,与第一章布尔代数公式形成呼应:
联结词 | 符号 | 真值规则(A、B为原子命题) | 示例(结合第一章案例) |
否定 | 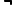
| 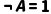 当且仅当 当且仅当 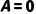
| 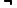 (晴天)= 阴天/雨天(真值与原命题相反) (晴天)= 阴天/雨天(真值与原命题相反)
|
合取(与) | 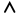
| 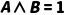 当且仅当 当且仅当 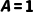 且 且 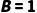
| P∧Q=“苏格拉底是人且所有人会死”(真值为真) |
析取(或) | 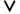
| 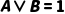 当且仅当 当且仅当 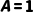 或 或 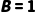 (可同时为真) (可同时为真)
| “有公交∨有地铁”=真(两种方式可同时存在) |
蕴含 | 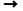
| 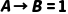 当且仅当 当且仅当 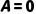 或 或 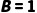 (仅A真B假时为假) (仅A真B假时为假)
| Q→P=“若所有人会死,则苏格拉底是人”(真值为真,与推理方向无关) |
等价 | 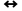
| 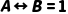 当且仅当 当且仅当 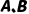 真值相同 真值相同
| “3是奇数↔5是奇数”(真值为真) |
1.3 命题演算的局限性(谓词演算的诞生原因)
命题演算虽能处理简单逻辑推理,但无法描述命题内部的语义结构,也无法表达“通用性”命题,这使其在AI复杂知识建模中存在明显不足,具体表现为两点:
无法拆分命题内部结构:例如“苏格拉底是人”和“柏拉图是人”,在命题演算中只能表示为两个独立原子命题P、Q,无法体现“苏格拉底”“柏拉图”都是“人”这一共同语义,导致知识冗余且无法捕捉共性规律。
无法表达量化关系(通用性/存在性):无法描述“所有人会死”“存在一个偶数是质数”这类含“所有”“存在”的命题,而这类命题是人类推理的核心(如第一章三段论的大前提“所有人会死”)。
正是这些局限性,催生了谓词演算——通过引入“个体”“谓词”“量词”,精准捕捉命题内部语义和量化关系,成为AI符号表示的核心语言。
二、谓词演算的核心:语法与语义
谓词演算的语法定义了“如何正确构建表达式”,语义定义了“表达式的真值如何确定”,二者结合确保形式化语言既能精准建模知识,又能进行有效推理。
2.1 谓词演算的基本语法元素
谓词演算的语法元素分为六类,层层组合形成合法表达式(合式公式):
函数(Functions):对个体进行映射,返回一个新个体(区别于谓词:谓词返回真值,函数返回个体),用小写英文字母f、g、h表示,参数为个体。示例:f(x)=“x的父亲”(x是个体,f(x)返回x的父亲这一个体),g(x,y)=“x+y”(返回x与y的和)。
量词(Quantifiers):约束个体变量的范围,解决命题演算无法表达量化关系的问题,核心有两类:
逻辑联结词:与命题演算一致,包括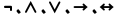 ,用于组合原子谓词公式形成复合谓词公式。
,用于组合原子谓词公式形成复合谓词公式。
辅助符号:括号()、逗号,用于明确表达式的运算优先级和参数分隔,避免歧义。
2.2 谓词演算的合式公式(WFF):合法表达式规则
合式公式是谓词演算中“有意义”的合法表达式,需遵循以下递归规则构建,确保语法正确:
原子谓词公式是合式公式:若P是n元谓词,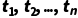 是个体项(个体常量/变量/函数),则
是个体项(个体常量/变量/函数),则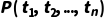 是合式公式(如P(a)、R(x,f(y)));
是合式公式(如P(a)、R(x,f(y)));
若A是合式公式,则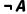 也是合式公式(如
也是合式公式(如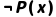 );
);
若A、B是合式公式,则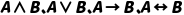 均是合式公式(如
均是合式公式(如 );
);
若A是合式公式,x是个体变量,则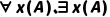 均是合式公式(如
均是合式公式(如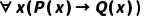 );
);
仅通过以上规则有限次推导得到的表达式,才是合式公式(排除歧义表达式,如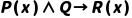 ,需加括号明确优先级)。
,需加括号明确优先级)。
2.3 谓词演算的语义:确定表达式的真值
语义的核心是“给合式公式赋值”,即通过定义“论域”和“解释”,确定公式的真值(1/0)。不同于命题演算直接给原子命题赋值,谓词演算的语义需结合个体、谓词、函数的具体含义。
给每个个体常量赋值:指定论域D中的一个元素(如a=苏格拉底,对应D=“所有人”中的苏格拉底);
给每个n元谓词赋值:指定一个从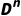 (D的n次笛卡尔积)到{0,1}的映射(如P(x)=“x是人”,映射规则为“若x是D中的人则为1,否则为0”);
(D的n次笛卡尔积)到{0,1}的映射(如P(x)=“x是人”,映射规则为“若x是D中的人则为1,否则为0”);
给每个n元函数赋值:指定一个从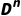 到D的映射(如f(x)=“x的父亲”,映射规则为“返回x在D中对应的父亲个体”)。
到D的映射(如f(x)=“x的父亲”,映射规则为“返回x在D中对应的父亲个体”)。
关键结论:谓词演算公式的真值依赖“论域+解释”,同一公式在不同论域或解释下可能有不同真值;若公式在所有论域和解释下均为1,称为“永真式”(如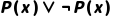 );若均为0,称为“永假式”(如 );若均为0,称为“永假式”(如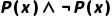 );否则为“可满足式”。 );否则为“可满足式”。 |
三、谓词演算的核心推理规则:实现逻辑推导
推理规则是谓词演算实现“从已知知识推导出新知识”的核心工具,本章重点讲解3类基础规则:命题演算推理规则的推广、量词消去/引入规则、合一算法,三者结合构成AI符号推理的基础流程。
3.1 命题演算推理规则的推广
命题演算的所有推理规则(如假言推理、拒式假言推理、德摩根定律等)均可直接推广到谓词演算,只需将“原子命题”替换为“谓词演算合式公式”,核心规则如下:
3.2 量词相关推理规则(消去与引入)
由于谓词演算含量词,需额外补充“量词消去”(将量化公式转化为非量化公式,便于推理)和“量词引入”(将推理结果还原为量化公式,实现通用结论)规则,共4条核心规则,需严格遵循约束条件避免错误。
3.2.1 全称量词消去规则(UI:Universal Instantiation)
规则内容:若已知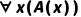 (对所有x,A(x)为真),则可推出
(对所有x,A(x)为真),则可推出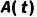 ,其中t是任意个体项(常量、变量、函数),且t对A(x)中的x是自由的(即t替换x后不会被其他量词约束)。
,其中t是任意个体项(常量、变量、函数),且t对A(x)中的x是自由的(即t替换x后不会被其他量词约束)。
示例:已知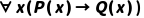 (所有人会死),可推出
(所有人会死),可推出 (苏格拉底会死)、
(苏格拉底会死)、 (任意x是人则会死)、
(任意x是人则会死)、 (x的父亲是人则会死)。
(x的父亲是人则会死)。
约束提醒:若A(x)中x在量词 或
或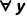 的辖域内,t不能是y(如
的辖域内,t不能是y(如 ,不能用y替换x,否则会出现
,不能用y替换x,否则会出现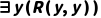 ,改变原公式语义)。
,改变原公式语义)。
3.2.2 全称量词引入规则(UG:Universal Generalization)
规则内容:若已知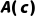 (c是论域中任意一个个体常量,A(c)为真),则可推出
(c是论域中任意一个个体常量,A(c)为真),则可推出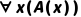 。
。
示例:若论域D=“所有人”,已知c是任意一个人(非特定个体),且A(c)=“c会死”为真,则可推出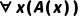 (所有人会死)。
(所有人会死)。
约束提醒:c必须是“任意个体”,不能是特定个体(如仅知道“苏格拉底会死”,不能直接推出“所有人会死”);且A(c)中不能含依赖c的前提条件。
3.2.3 存在量词消去规则(EI:Existential Instantiation)
规则内容:若已知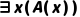 (存在x使A(x)为真),则可推出
(存在x使A(x)为真),则可推出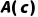 ,其中c是论域中一个“新的、未被使用过的个体常量”(称为“Skolem常量”)。
,其中c是论域中一个“新的、未被使用过的个体常量”(称为“Skolem常量”)。
示例:已知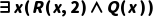 (存在大于2的偶数),可推出
(存在大于2的偶数),可推出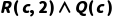 (c是某个大于2的偶数,如4、6等,且c未在之前推理中使用过)。
(c是某个大于2的偶数,如4、6等,且c未在之前推理中使用过)。
约束提醒:c必须是新常量,不能是已使用的常量或变量(如不能用a=苏格拉底替换,否则会将“存在一个偶数”错误绑定为“苏格拉底是偶数”)。
3.2.4 存在量词引入规则(EG:Existential Generalization)
规则内容:若已知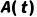 (t是任意个体项,A(t)为真),则可推出
(t是任意个体项,A(t)为真),则可推出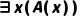 ,其中x是未在A(t)中出现过的个体变量。
,其中x是未在A(t)中出现过的个体变量。
示例:已知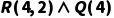 (4是大于2的偶数),可推出
(4是大于2的偶数),可推出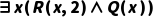 (存在大于2的偶数)。
(存在大于2的偶数)。
3.3 合一算法(Unification Algorithm):推理的核心工具
合一算法是谓词演算推理的关键,核心目标是“找到一个个体项替换集合(置换),使两个谓词公式变得相同”,从而触发推理规则(如假言推理)。例如,要将 与
与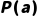 匹配,需通过置换
匹配,需通过置换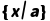 (将x替换为a),使
(将x替换为a),使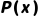 变为
变为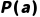 ,进而推出
,进而推出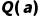 。
。
3.3.1 核心概念
3.3.2 最一般合一置换(MGU)的判定与算法步骤
MGU的求解是合一算法的核心,仅当两个谓词公式满足“谓词符号相同、元数相同”时才可能合一(如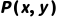 与
与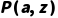 可合一,
可合一,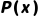 与
与 不可合一)。以下是标准化算法步骤(适用于绝大多数谓词公式对):
不可合一)。以下是标准化算法步骤(适用于绝大多数谓词公式对):