结构的特征值屈曲是判断结构稳定承载力最基础最快速的方法。特征值屈曲的方程为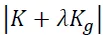
，其中K为结构的弹性刚度矩阵，Kg为外荷载作用下几何刚度矩阵，λ为特征值，该行列式对应方程组的非零解为结构的屈曲模态。对上述公式很长一段时间一直是似懂非懂，后来经老师的指导才恍然大悟。本文对该公式推导一遍，以加强理解。结构最基本的静力平衡方程为F=KU，当结构轴力较大时，结构的几何刚度矩阵不可忽略，此时结构的刚度矩阵变为K+Kg，且Kg随轴力的变化而变化，因此结构的荷载位移曲线变为非线性。结构的平衡方程变为增量形式，即∆F=(K+Kg)∆U。随着外荷载的变化，会出现刚度矩阵的行列式等于零的特殊情况，即|K+Kg|=0。此时∆F=(K+Kg)∆U的解不唯一，有通解和特解，其中通解便是对应的屈曲模态。下文推导过程可知，Kg与轴力或外荷载成正比，因此计算时，先算出某一特定荷载下的几何刚度矩阵，然后几何刚度矩阵乘以系数λ便为特定荷载乘以λ对应的几何刚度矩阵，通过求临界λ，便可求出临界外荷载。因此特征值屈曲的方程变为|K+λKg|=0。跟弹性刚度矩阵一样，结构的几何刚度矩阵Kg也是由单元的几何刚度矩阵”对号入座”组装起来的。以下采用能量法，推导桁架单元的弹性刚度矩阵和几何刚度矩阵。如下图所示，空间桁架单元，i节点和j节点发生位移
上式为单元节点力与节点位移的关系，记为：
一个结构中，各单元的单元坐标系一般不一致，无法直接组装成整体刚度矩阵，需通过坐标变换，将单元坐标系下的刚度矩阵转化为整体坐标系下的刚度矩阵。单元坐标系下的单位向量e与整体坐标系下单位向量e的关系如下：记为e=Te，T为坐标转换矩阵，且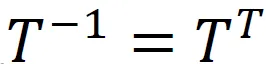
。则单元坐标系下的向量与整体坐标系下向量的关系如下：（1）预应力钢管混凝土柱，施加的预应力多少对钢管混凝土柱的稳定承载力几乎无影响；（2）自行车刹车时，细长的刹车线的自平衡力不会产生屈曲；（3）内压外拉的套管柱，其整体稳定承载力不会因为自平衡力提高或降低；（4）刚度矩阵的行列式为零，可以作为结构到达临界点的依据。DS公众号，敬请关注
www.directsolution.com.cn
DS真诚希望成为您的专业伴侣，
一起在专业的路上携手并进！
