基于弱形式推导有限元公式
前文已经介绍了一维结构的强形式和弱形式,本文将进一步探讨:弱形式如何一步步变成有限元的离散方程,也就是最终的。
1. 形函数的介绍
弱形式里我们需要两个函数:任意的权函数 (weight function)和未知的试解 (trial solution)。但计算机没法直接处理“任意函数”,因此有限元的第一步就是:在每个单元内,用一组简单的函数去逼近 和 。最常见的选择是多项式,例如在线性单元中可以假设:
问题在于:,这类系数只是数学参数,本身没有直观的物理意义,也不方便在多个单元之间建立连续性与耦合关系。
这就引出了形函数(shape function),也叫插值函数。形函数的核心作用是:把单元内的函数值用“节点值”表示出来——也就是把上面这些不直观的 换成具有明确物理意义的节点自由度。
1. 1D线性单元
让我们先看一个简单的例子。考虑一个单元 ,左右两个节点坐标为 和 ,节点值分别为。
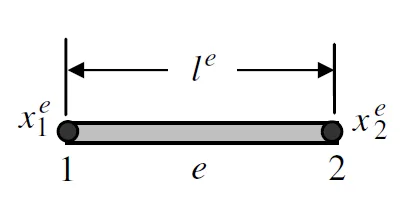
在单元内假设是一次多项式,即Eq.1所示。将其写成矩阵形式:
把节点条件代入(指这个多项式必须穿过两个节点):
将未知参数用节点值来表示即为:
将Eq.4代入到Eq.2中可得:
这一步非常关键:我们把未知函数 写成了形函数 与节点值 的线性组合。
以后我们只需要求节点未知量 , 函数就自动被确定了。
当单元长度 时,线性形函数为:
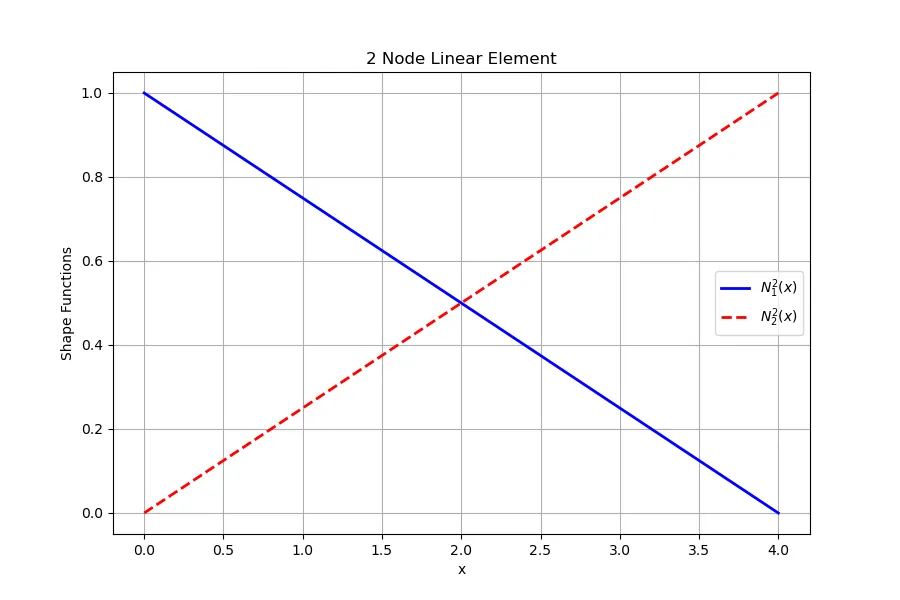
形函数的性质:插值性(Kronecker delta性质)
形函数最重要的要求是“插值性”:
直观理解:
2. 1D二次单元
对于二次1D单元,我们需要使用一个二次多项式:
它需要 3 个节点值才能唯一确定。实际推导我们可以继续用“矩阵求逆”的方式做(和线性单元完全同套路),但工程上更常用的写法是直接用拉格朗日插值(因为它天然满足 Kronecker delta 性质):
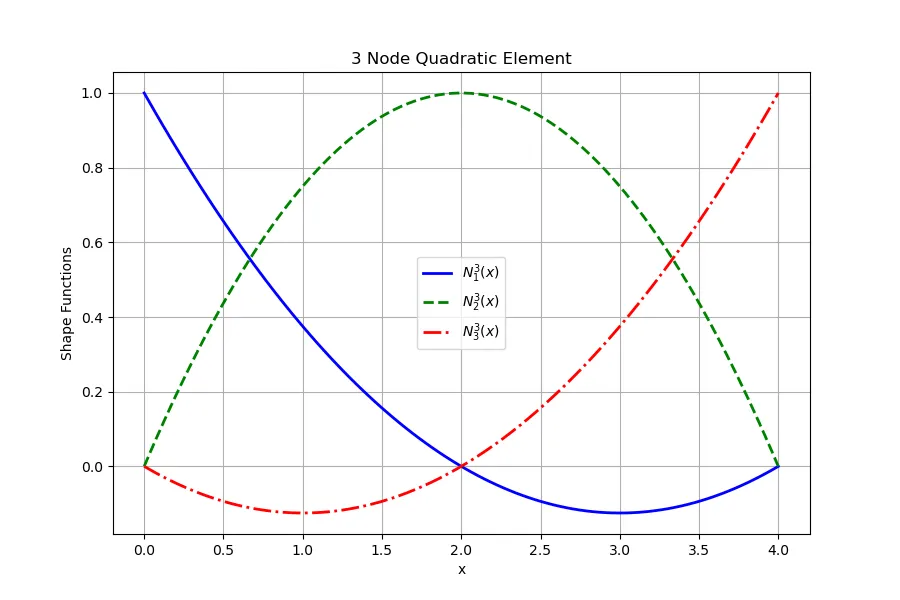
3. 1D三次单元
同理,1D三次单元(4 个节点)的形函数:
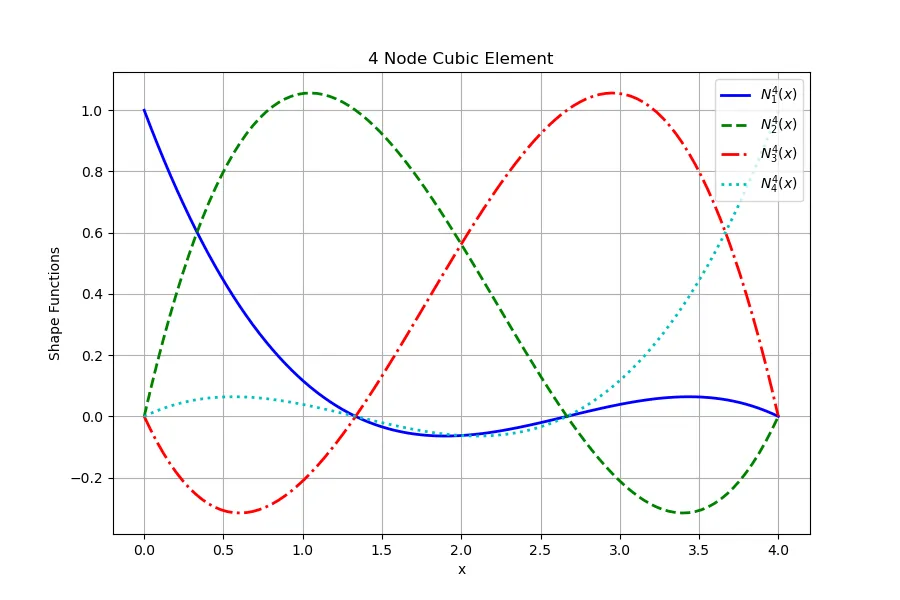
Galerkin FEM
试解和权重函数使用同一套形函数来逼近。这会让离散方程结构更规整,也常带来更好的性质(对称性/收敛性等)。
2. 从弱形式到有限元方程
一旦形函数构造完成,我们就可以将其代入弱形式中,从而推导出有限元方程。接下来,我们将逐步解释如何从弱形式得到离散的有限元方程。
首先,让我们回顾一下1D结构的弱形式。我们希望找到一个函数 ,它满足强制边界条件,并且满足以下条件:
其中 是标量,写转置只是为了和矩阵形式统一。
1. 网格划分:整体积分 = 单元积分之和
在有限元分析的前处理阶段,我们需要对结构进行网格划分。对于1D结构,网格划分相对简单。假设我们将结构 划分为 个单元,且共有 个节点。

接着,我们可以将原始的弱形式积分转换为每个单元的积分。也就是说,整个结构的积分可以表示为各个单元积分之和:
这一步只是把“整体问题”拆成“每个单元的小问题”。
2. 单元内代入形函数(Galerkin 离散)
在每个单元 中,试解和权函数都可以表示为形函数和节点值的线性组合:
将Eq.12代回弱形式Eq.11中,并把任意的 提出来:
由于 是任意的,上式可等价为:
其中单元的刚度矩阵可以通过积分得到:
外力矩阵由体力和边界力两部分组成:
3. 组装:从单元到整体
单元节点自由度是整体自由度的子集,用映射矩阵 表示为:
因此整体矩阵就是把每个单元的贡献“放回正确的位置”并求和:
最终得到全局离散方程:
4. 处理边界条件
把自由度按“已知位移”和“未知位移”划分:
同样把刚度矩阵与载荷向量按相同顺序分块:
将分块形式代入整体方程Eq.19得到:
注意 是已知的,所以真正用来求解未知位移的是第二行方程:
求得 ,我们可以用第一行回代得到本质边界上的约束反力(reaction force)。为了让反力在方程里有位置,我们把第一行写成:
于是反力为:
为输入的外力,在本质边界上我们指定位移,会产生未知反力 。
3. 举例:用FEM求解
1. 问题回顾
仍取前一篇推文中的案例,具体参数:
本例中我们分别采用1和2个线性单元进行求解。
2. 单个线性单元求解
2.1 网格与自由度
一个单元覆盖整个杆:
节点自由度:
2.2 单元刚度矩阵
线性单元的形函数:
求导得 :
单元刚度矩阵:
2.3 单元等效结点力
体力项等效为结点力:
牵引在 端点,对应节点 1:
综上有:
2.4 施加本质边界并求解
整体方程(此时就是单元方程):
代入 可得:
最终的解为:
应力为:
用 1 个线性单元 FEM 得到的位移与应力,和上一篇用弱形式直接求得的“线性近似解”完全一致。
3. 两个线性单元求解
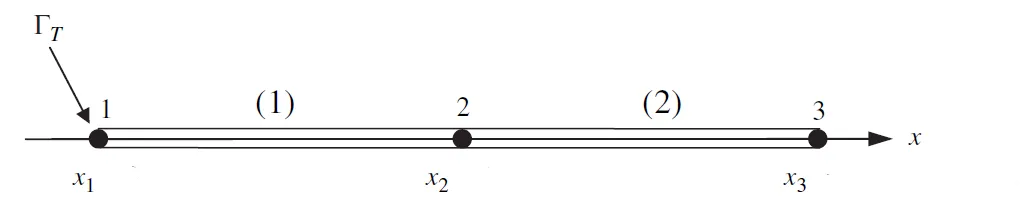
3.1 网格与自由度
将杆等分为两个单元:
自由度向量:
3.2 单元刚度矩阵
对任意线性单元 :
两个单元刚度矩阵均为:
3.3 单元等效结点力
单元1:
此时形函数:
体力等效结点力:
牵引边界只作用在 (节点 1):
所以单元 1 总等效结点力:
单元2:
此时形函数:
体力等效结点力:
单元 2 没有牵引边界项:,所以
3.4 组装整体方程
整体刚度矩阵(两单元组装):
整体载荷向量(把单元结点力加到对应全局节点上):
- • 节点 2:来自单元 1 的第 2 项 + 单元 2 的第 1 项
因此
整体方程为:
局部整体映射矩阵
由 可知,在该列中映射矩阵为:
3.5 施加本质边界并求解
写出前两行(第三行可用于反力):
第 1 行:
第 2 行:
代入 :
联立解得:
3.6 分段位移场与分段应力
单元 1():
单元 2():
最终结果的对比图如下所示:
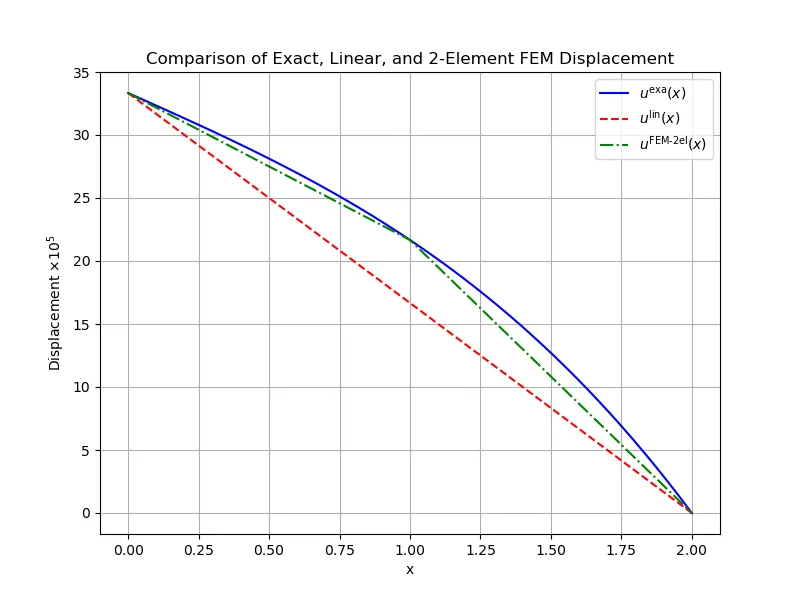
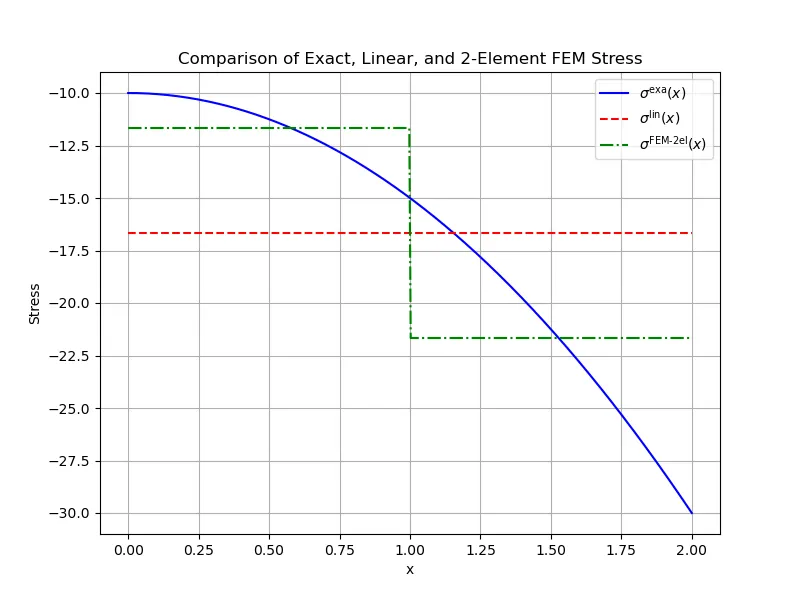
线性杆单元的位移在每个单元内为一次函数,因此应力在单元内为常数;不同单元的常数值一般不同,所以应力可在单元交界处跳跃,而位移仍保持连续。
因为 是本质边界(位移已知),会产生反力。第三行残差就是反力:
参考文献
- • Fish, Jacob, and Ted Belytschko. A First Course in Finite Elements. Wiley, 2007.