微积分通识学习笔记(三)蓝图

书接上话。

本篇推送包括以下六章节内容，带你直观的来构建微积分的蓝图。注：默认读者具有基础数学知识。

1、英文字母

2、希腊字母

3、数域

4、坐标系几何推演

5、曲线成面与曲面成体

6、逼近的艺术

让我们开始吧

这六部分，我会试着用文字和图像来引入，并且帛画你脑海中，关于微积分核心思想的大致蓝图。

PS：4、5、6会整合到一起阐述。

第一部分符号体系：

微积分中充斥着很多符号，他们几乎全部由两类构成。英文字母与希腊字母，并再辅以固定性特殊记号。

现将他们书写形式罗列如下。

1、英文字母（大小写）

2、希腊字母（大小写）

他们的读法表述如下：（汉化成普通人能读的，标准读法参考文末链接）

阿尔法 贝塔  伽马  德尔塔  伊普西隆  贼塔  （第1行）

伊塔  西塔  约塔  卡帕  拉木达  缪  （第2行）

纽  可赛  奥米克戎  派   肉  西格马  （第3行）

套夫 阿普西隆  费  楷  泼西   欧米伽  （第4行）

1和2内容小注：

英文字母和希腊字母常用来代指，后面常跟数字或变量或式子。再直白点说就是个“大号箱子”。

3、一些常见的固定记号有如下：

如上标 ′ 表示导数（f′为f的一阶导数）、( )^{(n)}表示高阶导数。

求和符号：∑（英文单词求和的缩写，可读作西格玛）

无穷符号：∞（表示“无限大”或“无界趋势”）

积分标志性符号为：∫ （表示要累加）

极限符号：lim（英文单词极限的缩写，可读作里米特）

微分标志性符号：「dx」及「dy」（difference有差距,差额的意思）

有限增量符号：小写形式为δ，大写形式为Δ

读音为"delta 汉语读：德尔塔"。

注：与微分符号d所代表的无限小增量不同，Δ主要用于描述有限小的增量或任意大的增量。

偏导数符号：∂ 

其角标数表示阶数，比如二阶偏导数（就是对变量求导数后再次求导）

4、一些常见的表示运算法则关系的符号有：

加减乘除：＋、－、×（·）、÷（∶）。微积分里常见的是他们的复合。

不等式关系：“>”（大于）、“<”（小于）、“>=”（大于等于）、“<=”（小于等于）、“==”（等于）、“!=”（不等于）

点积符号“·”与叉积符号“×”。在向量部分会涉及。

积分按照次数可分为一重积分、二重积分、三重积分，以及多重积分。相应符号为：∫、∫∫、∫∫∫。

没错，就是看符号个数。

第二部分数域体系：

有各种各样的数，他们构成各种各样的集体，就好像一个个人在巨大的广场上排排站一样，我们把他们的某一类的全部叫做数域。

有的时候他们彼此之间还有一定联系，比如某一类数是另一类数的特殊情况。

举个例子：实数可以看成是复数的一种特殊情况。

但通常情况下，大家都是分开讨论的。

1、现将数域划分如下。关于这些数域，微积分都会涉及到。

实数域：（实数）数轴上的所有全体。

复数域：带有i 的全体，表示为z=a+ib。其中a和b是实数，i是虚数单位。

有理数：能除尽或除不尽但周期循环，比如三分之一。

无理数：除不尽还不循环，比如π、√2等。

向量：可看作一种特殊的数，既有大小又有方向。区别于标量。

多项式：同样可看成一种特殊的数。

2、关于函数，初步介绍一下它。

它像一个机器一样，能吞进去一个数（原因），并且按照规则吐出另一个数（结果）。

对应符号为f。

也即函数能把一个数映射（按照规则）到另一个数上，把他们之间建立起关系（联系）来。

函数套函数，可以叫它复合函数。

通识课程（三）只考虑一些初等函数。广义函数不作涉及。

3、微积分的“式子里面”核心组成部分就是各种各样的函数（通常是复合函数）。

这里面的f(x)=各种各样的函数。

积分式子，要做的便是找原函数；微分式子，就是要求函数的导数。

根据找到的结果，一般意义上：

找的不确切的（不能唯一指定到某个的）一般叫“偏”的。比如偏导数，偏微分。

求导次数一般叫它阶数，比如二阶导数，二阶偏导数等。

注意：这是从大面上来理解的。

然后，我们可以把 1 纳入到 2 的体系，再把 2 纳入到 3 的体系中。

根据3（微积分的体系）就可以去研究现实世界中各类实际问题了（那些需要用到微积分的场景）。

注：当然1和2本身也可以研究很多比较简单的问题。（中学以下内容）

4、关于函数方程的解。

初阶：都是数，某个具体的数（小学，初中，高中部分）

进阶：某一类数或表达式（初中，高中，大学部分）

高阶：（函数）解系，没错就是解的解，它能是函数或一种式子，解能构成一个系列。（大学以上，如广义函数/泛函分析部分研究内容）

举例子：

比如0解、非0解，有限解、无限多解，基础解系、用有限结构解表示无限解。

微积分的解涉及所有的初阶和进阶，包括一部分高阶。（这里指一般的微积分）

第三部分各种坐标系：

好比人住在房子里一样，数也有自己的特殊房子。某一类数域的“房子”可以叫它坐标系。

PS部分坐标系维数有：包括0维、1维、2维、3维，掌握3维就足够了。（0维：点；1维：线；2维：面；3维：常见几何体）

根据研究对象或适应场景，相适应的坐标系分为。

1、空间直角坐标系

2、复数坐标系（复平面）

3、极坐标系

4、球坐标系

5、柱坐标系

微积分涉及到的坐标系就是以上5种。

第四部分各种各样的点线面空间几何体：

有了坐标系的几何形象概念后，于是我们可以在这些”房子“里画出各种图形。

有闭合的，有非闭合的；有直的，有曲的；有点的，有线的，有面的，有立体的；有能画完的，有画不完的。

别忘了，这些图形本质上是数构成的集合。

数形结合，是学习高数的一大法门。（对应空间解析几何的内容）

1、特殊地，如果以直角坐标系为研究对象，我们就可以画出一些图形来。

那么主要有以下这几大类。

第一大类：点

1这些点都在数轴上

2这些点都在平面上（有序数对）

3这些点有的落在数轴上，有的在平面上

但他们都是一类特征：都是一个个的点。

第二大类：线

如果把任意几个点串联成一条直线，那么常见的有这些情形。

1是平的

2是倾斜的

3是折的

第三大类：曲线

如果这些线是弯曲的，那么可以画成这样

1任意曲线

2规则曲线（圆、抛物线、双曲线、椭圆、指数函数等）

第四大类：面

如果在其上画出一个个面，那么同样，有这些形状

1任意曲面

2规则形状（圆、椭圆、矩形、三角形等）

同样的，如果我们升维，那么面经过平移或旋转，就可以在空间中画出一个个立体“几何体”出来。

你应该发现了，在坐标系中，你可以连点成线，连线成面，连面成体。

以下这些是我们所熟悉的。

那么，对于既有的规则图形和几何体，我们有公式体系去对付他们，那么碰到一些诸如曲线围成的面积，或者不规则的立方体，该如何呢？

比如这个：

我们并不是束手无策。

2、我们可以试着从微观上入手，引入极限，积少成多，分割与再整合的艺术，采用从量变到质变的方法。

并沿着1归纳、→2掌握、→3推广其中所蕴含的“方法和道理”，这条路径就是微积分中核心研究逻辑之一。

3、整合开篇中的5和6，对于这些图形家族来说：（以下是本期通识课程三的精华内容）

情况一，对于平面或空间规则的图形，初高中有很多求面积、求体积公式，我们有很多方式去对付他们。（对应小学初中高中求面积求体积公式）

情况二，对于带有曲线的图形，该怎么去求面积呢？甚至于在空间中求其体积呢？

比如：

可以从微观上分割他们，采用极限思想

积少成多似乎是个很好的方法

同样的方法，可以推广研究很多种类型的曲线下的面积。（想象一下：你可以把平面情况拓展到空间上，就成了曲面所构成的几何体——这个屋顶是曲面，四周是规则的）

如图，这个就是第一型曲面积分。

再一般化的，这个

这个你可以思考一下

话说到这里，由情况二入门微积分是个很好的路径。

深入地，由二次曲面构成的（平移+旋转）12类几何体，本期微积分通识课程（三）不做讨论

情况三，对于一些超越初等函数能力范围外的，又怎么去求面积呢？比如随便大手一挥画一个无规律的曲线（你可以想象），该用什么函数去复刻它呢？

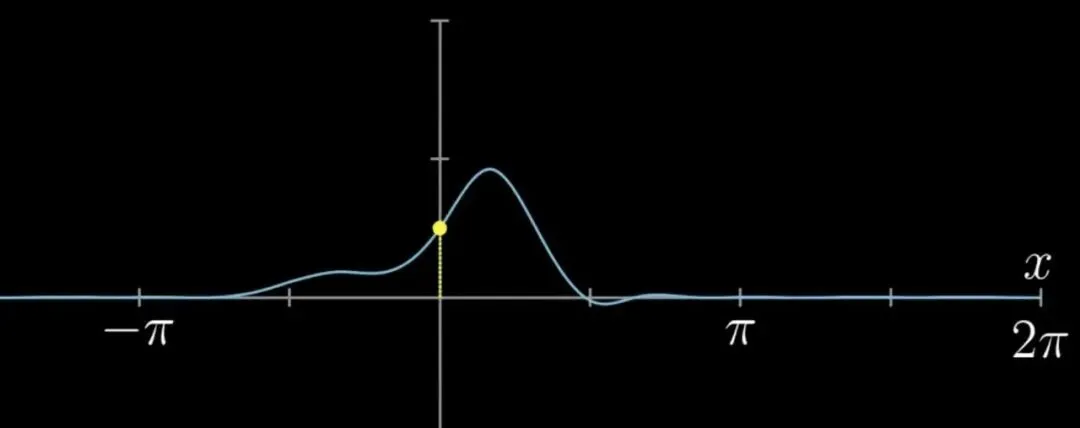
我们也有办法，那就是引入多项式，进而引入级数。（在这里请记住泰勒这个名字）

级数就是多项式函数，是多项式的一种推广。（泰勒多项式与泰勒级数）

特点，好求导、好积分。能力：用来逼近原函数。

举个例子：

有的时候，由于曲线画的太过复杂，超过了一些已知的、常用的或者能找到的函数的能力范围，那么不用担心，我们还可以试着去逼近它，这就是级数发挥威力的时候了。

先看用级数去近似（或叫逼近）初等函数。

多项式（右）逼近

级数与近似

只要你愿意，你可以试着在这个多项式后面按照规律不断加上一些“式子”，那么你就可以不断去逼近原图形。（前提是要收敛）

请看这个动图展示。

没错，级数很大程度上的一种能力就是去逼近这些曲线。（前提是在收敛半径上）

后面的项数越多（右）与原曲线越逼近（左）

发散（逼近边界）与收敛半径（近似范围）

再来看，曲线再一般化一些：

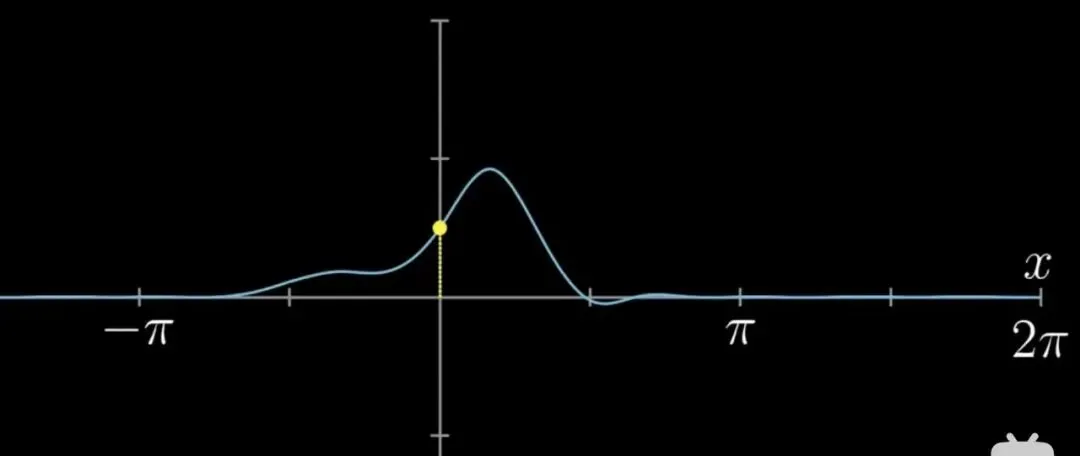
没事儿，可以用这个控制按钮去一般化多项式：

用白线去逼近原图像：是不是好像还不错，挺丝滑的

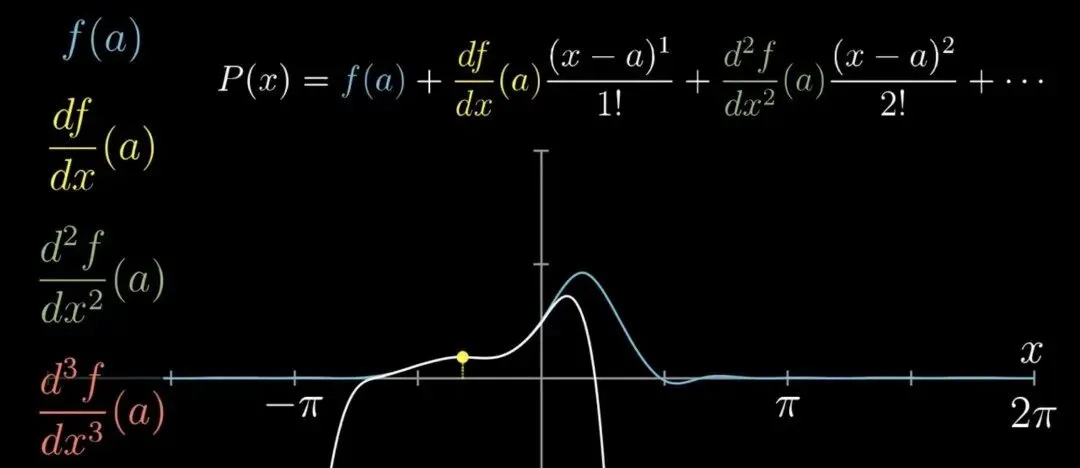
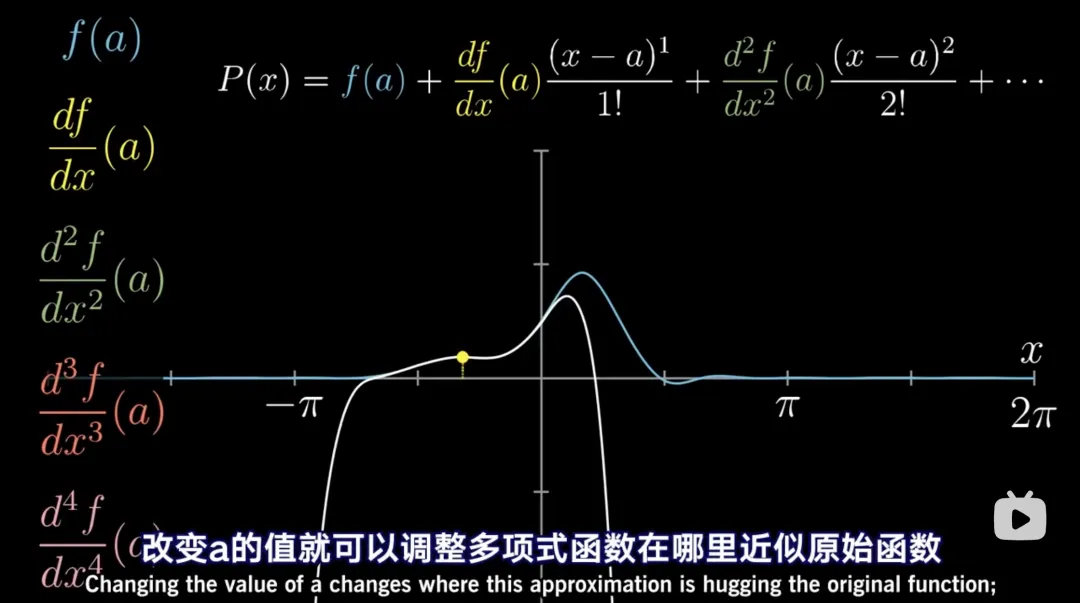
想象一下，推而广之，同样成立，不信你可以去验证。

逼近的关键就在于这些控制按钮。

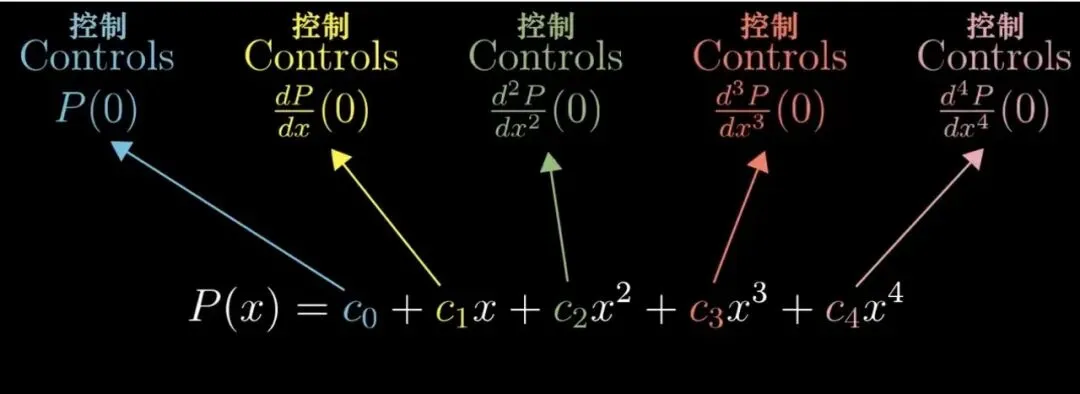
于是，当你对各样的曲线都不感到陌生与恐惧时，恭喜你，你已经知道了级数的强大威力了。

初等函数+导数+级数，这三大法宝足够让你去求很多的曲线围成的面积了。再由面积可以照应到（解释）现实世界的实际问题中去。

当然还有更复杂的图像，不过他们遵循是同样的道理。

这就是微积分通识课程为什么会在级数那里止步了。

好了，事实上，关于微积分的通识能认识到这一程度，已经足够告一段落了。

后续涉及到的更复杂的曲线、曲面（第一型和第二型：曲线交叉、重叠、闭合）的更一般化问题，（采用二重积分、三重积分思想）不在这部分通识笔记中涉及了。

不过，他们都是采用了分割与整合、转化的思想。

随着认识的深入，你可以去深究他们。

不过，本期内容可不会去“招惹”他们。

你能读到这里，很不错了。

到这里，你脑子里应该有微积分的大致蓝图了。虽然本期内容是尝试用文字+图形，带领你对微积分有个大致印象。

极限（分割）、累加（整合）、级数（逼近）

这三个家伙，是你擘画微积分世界的必备核心技能包。

我们把以上这些数学研究方法和思维方式应用到物理和化学中，就可以解决很多实际问题了。

微积分通识课程（三）（我想在你脑子里擘画的蓝图）

完

课后小甜点：

为了帮你更形象地理解微积分思想，请看在这里为你准备的两个例子。

例子一

图书馆桌子上的这桶瓶装水。

注意，它的瓶脖子处有开水烫过的痕迹，所以整个瓶子变得不规则。你可以把它看成空间不规则几何体。

但是，这一整瓶水是积少成多而灌满的，它是分割的足够细的一个个水面铺垫后，最终灌满了一瓶水。也就是由规则的水面一直加和，再加和不规则的水面，把这些都加和起来，于是，你就会得到一整瓶水。

例子二

你考上大学绝不是一蹴而就的。

它是建立在你对每一个知识点的分割上，而你日复一日的把每一个知识点都精确掌握和熟练运用后，最终通过“加和”，最终完成了一张满分试卷，并到达了、获得了你心仪的大学的入场券。

THE END 

附：

重点内容参考网络视频链接：（少打几盘王者，你将拥有一次美妙的数学体验）

希腊字母标准读法：

https://www.bilibili.com/video/BV1d44y147bT/?spm_id_from=333.337.search-card.all.click&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82

虚数和复数变量直观解释：

https://www.bilibili.com/video/BV1kX4y1u7GJ?spm_id_from=333.788.videopod.episodes&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82&p=12

点积和叉积直观解释：

https://www.bilibili.com/video/BV1kX4y1u7GJ?spm_id_from=333.788.videopod.episodes&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82&p=8

柱坐标与球坐标直观解释：

https://www.bilibili.com/video/BV1pVH9zfEFb/?spm_id_from=333.337.search-card.all.click&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82

微积分的本质直观解释：

https://www.bilibili.com/video/BV1qW411N7FU/?spm_id_from=333.337.search-card.all.click&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82

第一类和第二类曲面积分讲解：

https://www.bilibili.com/video/BV17GjUz4EUr/?spm_id_from=333.337.search-card.all.click&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82

由二次曲面构成的12类几何体：

https://www.bilibili.com/video/BV1NK411M7qM/spm_id_from=333.337.search-card.all.click&vd_source=4b74f1b171bb26c67a9d1c6c179c5b82