《1.1集合的概念》学习笔记

2026年2月4日星期三

今天初步学习了第一章的第一节，主要学习的是集合的概念，书中首先给出了一些具体的例子，借此来提炼、总结和辨析“集合”的概念。

1.集合的概念和特性

在做数学研究时首先要明确研究对象，而这个研究对象统称为元素，某些元素组成的总体就构成了集合。集合又具有一些特性：确定性（集合中的元素必须是确定的）、互异性（一个给定的集合中的元素的互不相同的）、无序性（集合中的元素没有顺序的）。只有同时具备这三个特性才能被称之为集合。

2.集合与元素的表示及关系

通常用大写拉丁字母A，B，C，…表示集合，用小写拉丁字母a，b，c，…表示集合中的元素。

如果a是集合A的元素，就说a属于集合A，记作a∈A；如果a不是集合A中的元素，就说a不属于集合A，记作 。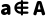

常用数集有特定的字母表示：自然数集N，正整数集N₊或N^*，整数集Z，有理数集Q，实数集R。

3.集合的三种表示方法

集合的表示方法主要有三种：自然语言、列举法、描述法。其中后两种在以后的学习中应用是比较多的，尤其是描述法。

在教材的第5页有一个思考题：举例说明，用自然语言、列举法和描述法表示集合时各自的特点。看到这里我想落笔写点什么，但是不知道怎么写，只知道用列举法表示的集合应该是有有限个元素的，描述法表示的集合中的元素是不可数的，不能一一列举出来的，但用自然语言表示的集合的特点是怎样的呢？我不不能组织语言表达出来。

整体来讲这一节偏重概念的理解，而要想深刻理解一些晦涩难懂、抽象的数学概念，最好是用比较熟悉和常用的例子进行辨析，所以我在想如果自己是高中老师来上这节课要怎样构思这节课的教学设计呢？我想我会在一些集合的例子上下功夫，让学生在认识了集合的概念后自己尝试举几个生活中表示集合的例子。有时间我也许会在网上找一找高中的数学公开课，看看高中老师是怎么上课的，自己的印象中当年高中学习都是照本宣科，毫无趣味可言。

最后想说一下自己做课后练习题的感受：首先这节课需要具备的基础知识总结如下：能够通过集合的特性来判断是否组成集合；会用数学符号表示元素与集合的关系；能根据集合的特点用合适的方式表示集合，主要是列举法和描述法。其次，在做教材第6页第4题时，有点感触：

（1）二次函数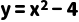的函数值组成的集合；

（2）反比例函数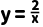的自变量的取值组成的集合；

看似两个问题并不难，但就现在的自己来讲我会圈画关键信息：要想表示集合，首先我要明确研究对象，这两道题都是从函数关系式入手，但是仔细观察就会发现，第（1）题是表示“函数值”组成的集合，而第（2）题表示“自变量的取值”组成的集合。这一细节是自己当年在学习时不曾关注到的，追究根本原因可能还是不理解“集合”的概念、元素与集合的关系，以及为什么高中数学刚开始学首先要学习集合的内容吧。但也正因如此，自己越来越坚定从小学数学就要培养学生认真审题的好习惯是非常有必要的，而且能够从小就学会用思维导图把零散的数学知识进行系统化的梳理对于未来初高中的学习是非常有利的。