n
章末检测试卷二(第七章)
[时间:120分钟 分值:150分]
一、单项选择题(本题共8小题,每小题5分,共40分)
1.(2023·新高考全国Ⅰ)已知z=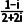 ,则z-
,则z-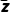 等于( )
等于( )
A.- iB.iC.0D.1
答案 A
解析因为z=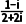 =
=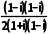
=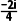 =-
=-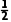 i,所以
i,所以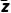 =
=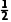 i,
i,
即z-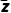 =-i.
=-i.
2.(2023·新高考全国Ⅱ)在复平面内,(1+3i)(3-i)对应的点位于( )
A.第一象限B.第二象限
C.第三象限D.第四象限
答案 A
解析因为(1+3i)(3-i)=3+8i-3i2=6+8i,
则所求复数在复平面内对应的点为(6,8),位于第一象限.
3.若z1,z2为复数,则“z1+z2是实数”是“z1,z2互为共轭复数”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 B
解析由题意,不妨设z1=a+bi,
z2=c+di(a,b,c,d∈R),
若z1+z2是实数,则z1+z2=a+bi+c+di=(a+c)+(b+d)i∈R,
故b+d=0,即b=-d,
由于a,c不一定相等,故z1,z2不一定互为共轭复数,故充分性不成立;
若z1,z2互为共轭复数,则z2=a-bi,
故z1+z2=2a∈R,故必要性成立.
因此“z1+z2是实数”是“z1,z2互为共轭复数”的必要不充分条件.
4.设i是虚数单位,x是实数,若复数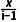 的虚部是2,则x等于( )
的虚部是2,则x等于( )
A.4B.2C.-2D.-4
答案 D
解析复数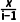 =
=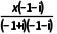
=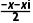 =-
=-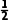 x-
x-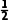 xi,
xi,
∵复数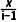 (x∈R)的虚部为2,
(x∈R)的虚部为2,
∴-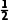 x=2,∴x=-4.
x=2,∴x=-4.
5.(2022·全国乙卷)已知z=1-2i,且z+a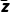 +b=0,其中a,b为实数,则( )
+b=0,其中a,b为实数,则( )
A.a=1,b=-2B.a=-1,b=2
C.a=1,b=2D.a=-1,b=-2
答案 A
解析由题意知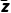 =1+2i,
=1+2i,
所以z+a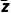 +b=1-2i+a(1+2i)+b
+b=1-2i+a(1+2i)+b
=a+b+1+(2a-2)i,
又z+a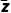 +b=0,且a,b∈R,
+b=0,且a,b∈R,
所以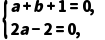 解得
解得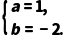
6.设复数z1,z2在复平面内的对应点关于虚轴对称,且z1=3-2i,则|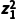 +z2|等于( )
+z2|等于( )
A.2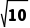 B.5
B.5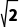 C.3
C.3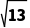 D.10
D.10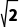
答案 D
解析由题意得,z2=-3-2i,
∴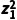 +z2=(3-2i)2+(-3-2i)
+z2=(3-2i)2+(-3-2i)
=5-12i-3-2i=2-14i,
∴|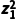 +z2|=
+z2|=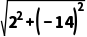 =10
=10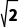 .
.
7.复数z=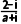 (a∈R)为纯虚数,则|2a+
(a∈R)为纯虚数,则|2a+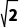 i|等于( )
i|等于( )
A.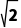 B.
B.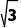 C.2
C.2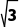 D.3
D.3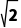
答案 B
解析因为z=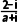 为纯虚数,
为纯虚数,
所以设z=bi(b∈R,b≠0),
即bi=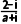 ,则bi(a+i)=2-i,
,则bi(a+i)=2-i,
因此-b+abi=2-i,
从而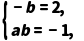 即
即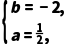
所以|2a+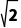 i|=|1+
i|=|1+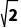 i|=
i|=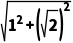 =
=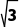 .
.
8.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式eix=cos x+isin x(e是自然对数的底数,i是虚数单位),这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”.下列说法正确的是( )
A.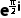 +1=0B.
+1=0B.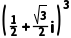 =1
=1
C.cos x=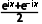 D.sin x=
D.sin x=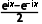
答案 C
解析对于A,当x=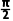 时,
时,
因为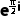 =cos
=cos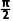 +isin
+isin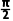 =i,
=i,
所以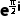 +1=i+1≠0,选项A错误;
+1=i+1≠0,选项A错误;
对于B,=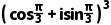
=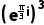 =eπi=cosπ+isinπ=-1,选项B错误;
=eπi=cosπ+isinπ=-1,选项B错误;
对于C,由eix=cosx+isinx,
得e-ix=cos(-x)+isin(-x)=cosx-isinx,
所以eix+e-ix=2cosx,
得出cosx=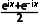 ,选项C正确;
,选项C正确;
对于D,由C选项的分析得eix-e-ix=2isinx,得出sinx=-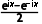 i,选项D错误.
i,选项D错误.
二、多项选择题(本题共3小题,每小题6分,共18分.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知i为虚数单位,下列说法中正确的是( )
A.若复数z满足|z-i|=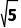 ,则复数z在复平面内对应的点在以(1,0)为圆心,
,则复数z在复平面内对应的点在以(1,0)为圆心,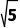 为半径的圆上
为半径的圆上
B.若复数z满足z+|z|=2+8i,则复数z=-15+8i
C.若复数z1,z2满足|z1|=|z2|,则z1·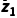 =z2·
=z2·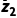
D.若复数z1,z2满足|z1|=|z2|,则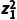 =
=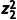
答案 BC
解析满足|z-i|=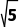 的复数z在复平面内对应的点在以(0,1)为圆心,
的复数z在复平面内对应的点在以(0,1)为圆心,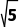 为半径的圆上,故A错误;
为半径的圆上,故A错误;
设z=a+bi(a,b∈R),
则|z|=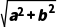 ,由z+|z|=2+8i,
,由z+|z|=2+8i,
得a+bi+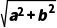 =2+8i,
=2+8i,
故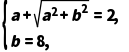 解得
解得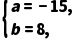
∴z=-15+8i,故B正确;
设z1=a1+b1i,z2=a2+b2i,a1,b1,a2,b2∈R,
若|z1|=|z2|,则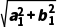 =
=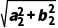
即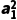 +
+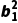 =
=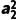 +
+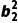
∴z1·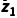 =
=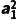 +
+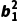 =
=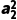 +
+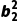 =z2·
=z2·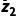 ,故C正确;
,故C正确;
若z1=1,z2=i,则|z1|=|z2|,
而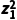 =1,=-1,故D错误.
=1,=-1,故D错误.
10.已知集合M={m|m=in,n∈N*},其中i为虚数单位,则下列元素属于集合M的是( )
A.(1-i)(1+i)B.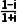
C.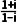 D.(1-i)2
D.(1-i)2
答案 BC
解析根据题意,M={m|m=in,n∈N*},
当n=4k(k∈N*)时,in=1;
当n=4k+1(k∈N)时,in=i;
当n=4k+2(k∈N)时,in=-1;
当n=4k+3(k∈N)时,in=-i,
∴M={-1,1,i,-i}.
选项A中,(1-i)(1+i)=2∉M;
选项B中,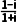 =
=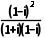 =-i∈M;
=-i∈M;
选项C中,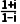 =
=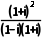 =i∈M;
=i∈M;
选项D中,(1-i)2=-2i∉M.
11.已知z1,z2∈C,下列命题正确的是( )
A.|z1|2=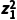
B.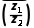 =
=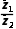 (z2≠0)
(z2≠0)
C.若z1·z2=0,则z1,z2至少有1个为0
D.若z1,z2是两个虚数,z1+z2∈R,z1·z2∈R,则z1,z2为共轭复数
答案 BCD
解析设z1=a+bi,z2=c+di,a,b,c,d∈R.
对于选项A,例如z1=i,则|z1|2=1,=-1,
显然|z1|2≠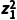 ,故A错误;
,故A错误;
对于选项B,因为z2≠0,
则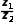 =
=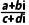 =
=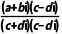 =
=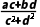 +
+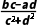 i,
i,
可得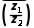 =
=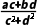 -
-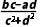 i;
i;

通过网盘分享的文件:同步PPT课件等3个文件
链接: https://pan.baidu.com/s/1ZlSxnGdFezeT3YPAHstUhQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享