 n
n
章末素养提升
物理 观念 | 曲线运动 | 定义 | 物体运动的是的运动 |
特点 | ①轨迹是;②曲线运动的时刻在改变;③曲线运动一定是运动 |
速度的 方向 | 质点在某一点的速度方向,沿曲线在这一点的 |
做曲线运 动的条件 | 当物体所受的合力的方向与它的速度方向时,物体做曲线运动 |
运动的合 成与分解 | 由分运动求合运动的过程,叫作运动的合成 |
由合运动求分运动的过程,叫作运动的分解 |
运动的合成与分解遵循 |
抛体运动 | 定义 | 以将物体抛出,在空气阻力的情况下,物体只受作用,这时的运动叫作抛体运动 |
分类 | ①竖直上抛;②竖直下抛;③平抛;④斜抛 |
平抛运动 | 定义 | 初速度沿方向的抛体运动 |
特点 | ①初速度沿方向;②只受作用 |
性质 | 加速度为g的曲线运动 |
规律 | ①在水平方向上的分运动是运动 ②在竖直方向上的分运动是运动 |
两个重 要推论 | 做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过水平位移的中点 |
做平抛运动的物体在某时刻,设其速度与水平方向的夹角为θ,位移与水平方向的夹角为α,则 |
类平抛运动 | 合外力且于初速度方向的运动都可以称为类平抛运动 |
科学 思维 | 物理建模 | 将运动分解为沿合力方向的匀加速直线运动和垂直合力方向的匀速直线运动,两个分运动彼此独立、互不影响,且与合运动具有等时性 |
通过分解平抛运动,学生加强“化曲为直、化繁为简”的思想 |
逆向思维解决抛体运动 | 把运动过程的“末态”当成“初态”来反向研究问题的方法 |
逻辑推理 | 有约束条件的平抛运动 |
平抛临界问题 |
抛体运动规律的综合应用 |
科学 探究 | 1.参与小船渡河、蜡块运动的探究,体验科学探究的一般过程 2.利用对比分析方法或频闪技术得到平抛运动轨迹 3.通过合作探究平抛运动的规律,培养学生的探究精神和合作精神 |
科学 态度 与责任 | 1.通过平抛运动规律的实践应用,意识到物理规律在现实生活中的重要作用,增强知识与实际生活联系的能力,增强对物理学习的兴趣,体验战胜困难、解决物理问题时的喜悦 2.逐步树立严谨科学的实验态度和正确的人生观 |
| | | |
例1(2023·聊城市高一期末)如图所示为中国无人机“翼龙”飞行时的照片。无人机巡航时水平分速度为40 m/s,竖直分速度为0。无人机接收到动作指令后立即在竖直方向上做匀加速直线运动,在水平方向上仍以40 m/s的速度做匀速直线运动。以无人机接收到动作指令为计时起点,当无人机运动的水平位移为160 m时,其竖直位移也为160 m,关于这一过程,下列说法正确的是()
A.无人机的运动轨迹为直线
B.无人机运动的时间为8 s
C.无人机的加速度大小为20 m/s2
D.此时无人机的速度为80 m/s
例2某排球队在某运动会中取得了辉煌的成绩,这离不开教练的悉心指导和运动员们的刻苦训练。如图甲所示,是队员们对着竖直墙壁练习垫球的训练示意图。假设某次强化训练时,某队员在离墙4 m处把球在离地高1 m处以与水平方向成θ角垫出,球恰能垂直击中竖直墙上高为3 m的目标圈中心,如图乙所示。重力加速度g=10 m/s2,忽略空气阻力,则θ约为()
A.37°B.45°
C.53°D.74°
例3(2023·肇庆市高一期中)如图所示,滑板爱好者先后两次从坡道A点滑出,均落至B点,第二次的滞空时间比第一次长,则()
A.两次滑出速度方向相同
B.两次腾空最大高度相同
C.第二次滑出速度一定大
D.第二次在最高点速度小
例4(多选)(2024·安庆市高一期末)如图所示,某次空中投弹的军事演习中,战斗机在M点的正上方离地H高处以水平速度v1=0.9 km/s发射一颗炮弹1,经20 s击中地面目标P。若地面拦截系统在炮弹1发射的同时在M点右方水平距离x=1 500 m的地面上的N点,以速度v2竖直发射拦截炮弹2恰好成功拦截。若不计空气阻力,g取10 m/s2,下列说法正确的是()
A.战斗机发射炮弹时离地高度2 000 m
B.M点到P点的距离为1 800 m
C.炮弹从发射到拦截的时间为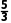 s
s
D.炮弹2的初速度大小v2=1.2 km/s
例5(2023·佛山市高一期中)食品加工厂包装饺子的一道工序可简化为如图所示模型,饺子离开传送带时与传送带共速,已知饺子抛出点A与接收槽口BC的高度差为h1,槽高为h2,槽壁厚度不计,传送带边缘与接收槽边缘的水平距离分别为x1和x2,现一质量为m的可视为质点的饺子离开传送带。忽略空气阻力,重力加速度为g。求:
(1)饺子从离开传送带到直接落在槽底的时间t;
(2)为保证饺子能落入槽口BC内,判断传送带运转速度范围。
答案精析
轨迹 曲线 曲线 速度方向 变速 切线方向 不在同一直线上 平行四边形定则 一定的速度 可以忽略 重力 水平 水平 重力 匀变速 匀速直线
自由落体 tan θ=2tan α 恒定 垂直
例1 C [无人机水平方向做匀速直线运动,竖直方向做匀加速直线运动,其合运动的轨迹为曲线,A错误;水平方向满足x=vt,解得运动的时间为t=4s,B错误;竖直方向满足y=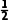 at2,解得a=20m/s2,C正确;vy=at=80m/s,v合=
at2,解得a=20m/s2,C正确;vy=at=80m/s,v合=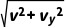 =40
=40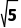 m/s,故D错误。]
m/s,故D错误。]
例2 B [排球运动的逆过程看作是平抛运动,则运动时间
t=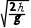 =
=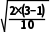 s=
s=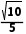 s
s
垫出时的竖直速度vy=gt=2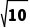 m/s
m/s
水平速度vx=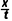 =
=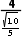 m/s=2
m/s=2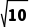 m/s
m/s
则tanθ=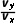 =1
=1
即θ=45°,故选B。]
例3 D [对运动员运动分析可知,从坡道A点滑出后,水平方向做匀速直线运动,竖直方向做竖直上抛运动,根据竖直上抛运动的对称性,即上升时间等于下降时间,由题知第二次的滞空时间比第一次长,所以第二次下降时间大于第一次,由h=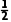 gt2知,第二次腾空最大高度大于第一次,又因为两次水平位移相等,所以两次滑出时的速度方向不相同,故A、B错误;因为第二次下降时间大于第一次,且两次水平位移相等,由x=vxt知,第二次滑出后水平分速度小于第一次,即第二次在最高点速度小,又由vy=gt可知,第二次滑出后竖直分速度大于第一次,所以第二次滑出速度不一定大,故C错误,D正确。]
gt2知,第二次腾空最大高度大于第一次,又因为两次水平位移相等,所以两次滑出时的速度方向不相同,故A、B错误;因为第二次下降时间大于第一次,且两次水平位移相等,由x=vxt知,第二次滑出后水平分速度小于第一次,即第二次在最高点速度小,又由vy=gt可知,第二次滑出后竖直分速度大于第一次,所以第二次滑出速度不一定大,故C错误,D正确。]
例4 ACD [炮弹1做平抛运动,竖直方向有H=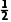 gt2=2000m,故A正确;
gt2=2000m,故A正确;
水平方向有x0=v1t,解得M点与P点的水平距离为x0=18km,故B错误;
炮弹1做平抛运动,炮弹2做竖直上抛运动,若要拦截成功,则两炮弹必定在空中相遇,竖直方向上有H=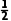 g
g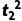 +(v2t2-
+(v2t2-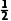 g
g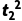 ),所以相遇时间t2=
),所以相遇时间t2=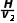 ,水平方向上,炮弹1做匀速直线运动,与炮弹2相遇的时间t1=
,水平方向上,炮弹1做匀速直线运动,与炮弹2相遇的时间t1=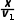 =
=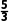 s,故C正确;
s,故C正确;
拦截成功时,有t1=t2,则v2=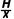 v1=1.2km/s,故D正确。]
v1=1.2km/s,故D正确。]
例5 (1)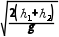 (3)x1
(3)x1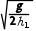 <v<x2
<v<x2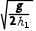
解析(1)饺子离开传送带后做平抛运动,直接落在槽底时,竖直方向有h1+h2=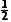 gt2,解得t=
gt2,解得t=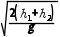
(2)设饺子在A点速度为v1时,饺子刚好到达C点,则有h1=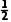 g
g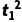 1=v1t1,解得v1=x1
1=v1t1,解得v1=x1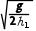 ,设饺子在A点速度为v2时,饺子刚好到达B点,则有h1=
,设饺子在A点速度为v2时,饺子刚好到达B点,则有h1=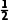 g
g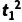 2=v2t1
2=v2t1
解得v2=x2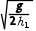 ,则为保证饺子能落入槽口BC内,传送带运转速度范围为x1
,则为保证饺子能落入槽口BC内,传送带运转速度范围为x1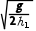 <v<x2
<v<x2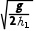 。
。

通过网盘分享的文件:【淘宝店:品优教学】赠送等3个文件
链接: https://pan.baidu.com/s/1B93EKvqf1fPyooILsCaxDg?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享