学习笔记2-雷朋汉定理和小库伦土压力公式

摘要

摘要：经过前文《学习笔记1》中的分析，可以看到将Ea对θ直接求导的推导求解土压力的难度很大，本文是一种巧妙的推导思路：基于平面几何等面积法原理，将原本 “求解角度 θ” 的核心问题，转化为更易操作的几何分析问题，引入两个引理从而简洁明了地推导出小库伦土压力计算公式，整个推导过程浅显易懂、条理清晰。关键词：平面几何，雷朋汉定理，挡墙土压力

引理1- 雷朋汉第一定理

雷朋汉第一定理：砂性土挡墙破裂楔体的面积，可等效转化为以内摩擦角所在边为依托并与力的矢量三角形相似的三角形面积进行计算。即下图图形ABC的面积等于△BCN的面积。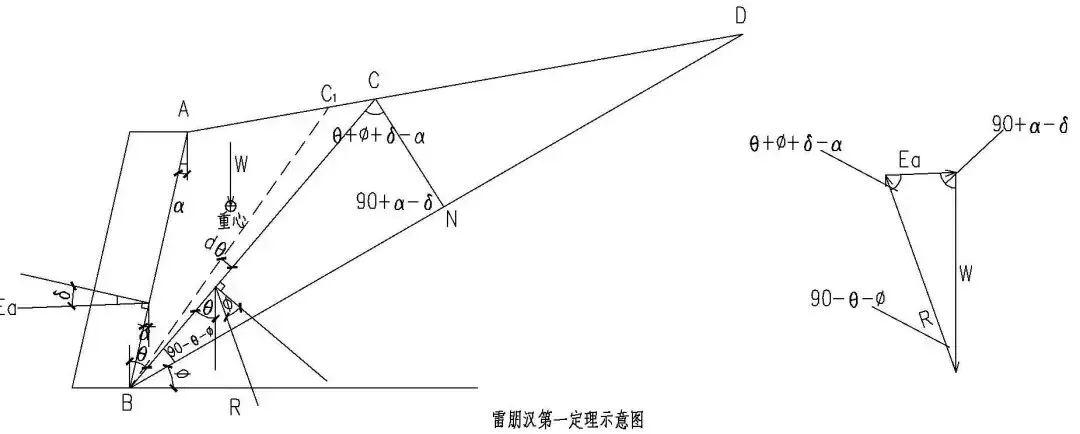证明：

• （1）易得，库伦土压力基本公式：
• （2）关键在于不带入W的详细表达式，直接将Ea对θ微分：

• （3）运用在破裂角位置处一定有 dEa/dθ=0,即(2)式=0，可得：

• （4）令破裂面处产生微小变量dθ，假设BC变到BC1，当破裂棱体为单位墙长时，破裂棱体重量减小量即为△BCC1面积的重量，即：

• （5）作直线CN使得有特殊角度∠BCN=θ+φ+δ-α，△BCN中由正弦定理有：

• （6）将（4）、（5）式带回（3）式可得：

即得证：面积（△ABC）=面积（△BCN）

引理2- 雷朋汉第二定理

雷朋汉第二定理：单位墙长的主动土压力等于土的容重乘以力三角形的面积。即Ea等于下图图形CNS面积的土重。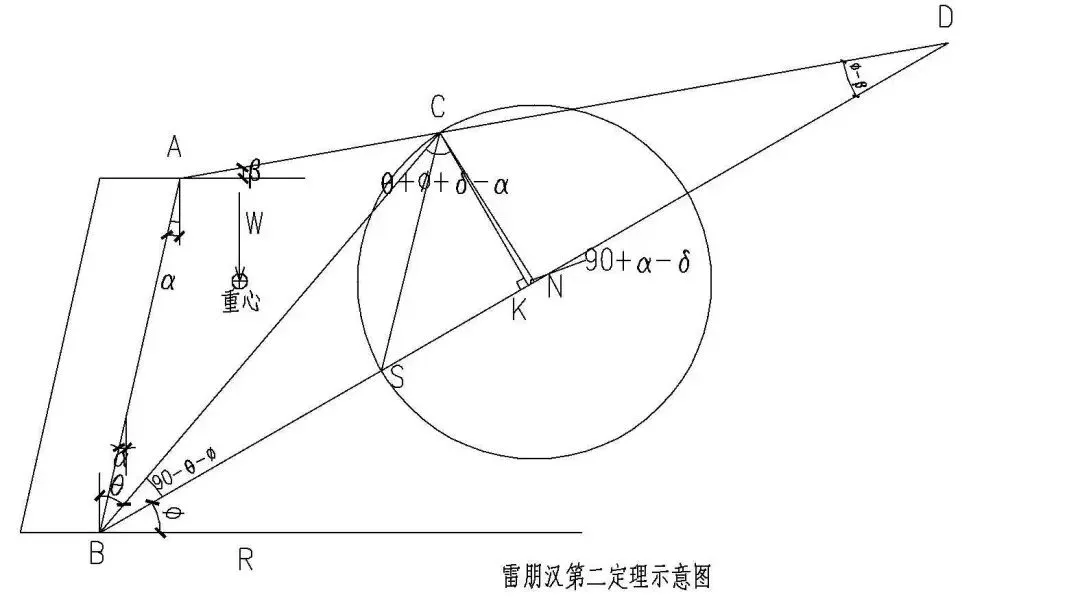证明

• （1）过点C作CK垂直BN于点K,由雷朋汉第一定理可得：

• （2）以N点为圆心，NC长为半径作圆，交BN于点S,由几何关系：

• （3）将（1）、（2）式带回库伦土压力基本公式可得：

小库伦土压力计算公式

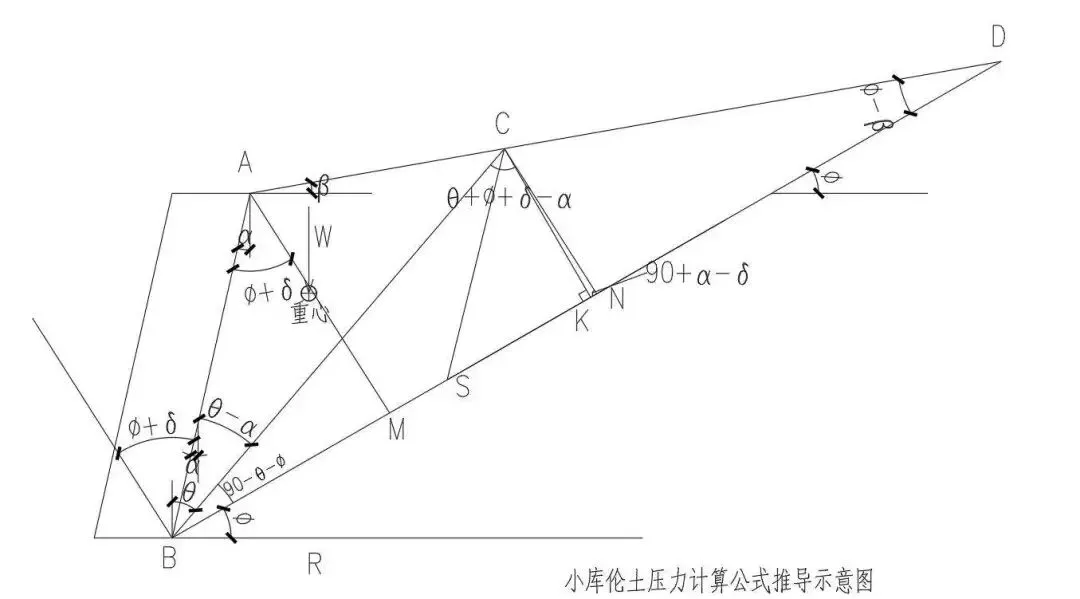
• （1）由平面几何知识可知：若两三角形同高，那么两三角形的面积比等于底之比,即：

• （2）由雷朋汉第一定理可知：面积（△ABC）=面积（△BCN），等量代换后有：

• （3）作AM平行于CN，交BN于点M,由平面几何的相似三角形性质有：

• （4）结合（2）、(3)式：

等价变形：

• （5）在三角形ABD中，点A、B、D、M的位置与破裂角θ无关，由挡墙倾角、内摩擦角、填土倾角、墙背摩擦角决定的，点C、N、S的位置与破裂角θ直接相关；若将带点C、N、S的线段长度可以用带点A、B、D、M的线段表示，那么理论上就可以绕开未知的破裂角θ，将三角形CNS的面积求出来，问题就迎刃而解了，由雷朋汉第二定理可知：

由几何关系有：

于是CN就可以绕开未知的破裂角θ，全部用ABMD四点的四条线段表示出来了，由几何关系易知：

通通带入雷朋汉第二定理Ea表达式即可得：

α为墙背竖直夹角，墙背仰斜取正，墙背仰斜取负；θ取的也为竖直破裂角。- END -

感谢我的身材，即使臃肿，我也能到世界各地去旅游；感谢我的鼻子，即使塌，也让我可以呼吸新鲜空气；感谢我的双眼，再小，再眯，我也能看见，日出，日落，花开，花谢。感谢太阳又升起，继续点燃我的梦想；感谢那些曾让我伤心难过的日子，我知道快乐已经离我不远了。——麦兜