本期会拆解CHAPTER F的内容
本章节共分为F1~F13
本章只适用于绕单一轴线弯曲的构件,在荷载作用点和支座处,这个构件也被限制不会发生扭转。

| F1: 一般规定 F2-F5: 工字型截面构件(按翼缘和腹板的不同分类 F6: 绕弱轴弯曲的工字型截面和槽钢 F7: 方形和矩形HSS及箱形截面 F8: 圆形HSS F9-F12: 各种角钢双角钢等截面 F13: 梁和主梁的比例 |
ØF1: 一般规定
和上一期一样,弯曲F章节上来也给了一个表格,这个表格的作用是帮助工程师快速根据你构件的特征来快速定位与你构件匹配的计算公式所在的小节号。仔细看这个表格。快速通过构件的section、腹板翼缘的屈曲抵抗能力和可能发生的极限状态快速定位到不同的章节,找到适合的设计规范条文。
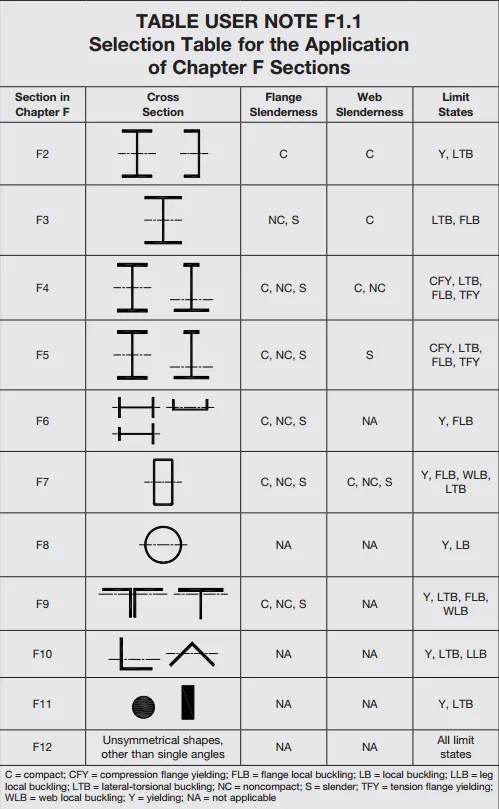
| C = compact 指截面具有足够的局部屈曲抵抗能力,在达到屈服强度前不会发生局部屈曲 NC = non compact 指截面在达到屈服前可能发生局部屈曲,但屈曲发生在屈服之后,即截面已经部分屈服了才发生屈曲 S = slender 指截面非常薄,在达到屈服强度前就会发生局部屈曲 CFY = compression flange yielding 是指会出现受压翼缘达到屈服强度的极限状态 FLB = flange local buckling 是指翼缘发生的局部屈曲现象的极限状态 LB = local buckling 是指截面某部分(翼缘或腹板)发生的局部屈曲的极限状态 LLB = leg buckling 是指角钢等截面肢件的屈曲的极限状态 LTB = lateral-torsional buckling 指梁在弯曲时发生的侧向位移和扭转组合屈曲的极限状态 TFY = tension flange yielding 是指受拉翼缘达到屈服强度的极限状态 WLB = web local buckling 指腹板发生的局部屈曲 |
F1中同样先给出了整个章节的既定性的定义和要求,首先就是名义屈服强度与两种设计方法的对应系数,详见条文(a);条文(b)则给出了整个F章节的计算假定:受弯构件在支座处被固定,在绕其纵向轴线的方向无法发生旋转,人话就是防止其产生侧向扭转屈曲LTB;条文(c)给出了适用于单曲率弯曲的单对称构件和双对称构件的侧向扭转屈曲修正系数Cb,其实就是将非均匀弯矩情况转换为均匀弯矩情况进行分析,需要注意notes里对双对称构件的Cb给出了简化计算结果,同时声明中对于单轴对称任何增加了详细说明,计算时很有参考价值;条文(d)要求单轴对称构件当产生反向弯曲曲率的时候,需要对两个翼缘都进行LTB强度的验证,是为了确保它不会因为LTB失稳。其实就是举例看就是T型构件,当它两头弯矩一正一负的时候,要对翼缘两侧都复核,避免产生侧向扭转失稳。包保证它的实际抗弯强度≥两侧翼缘的最大需求弯矩。

ØF2-F5: 工字型截面构件(按翼缘和腹板的不同分类)
F2~F5虽然都是工字型截面,他们分类的主要区别就在于翼缘和腹板不同的slenderness形态,其实也就是上文C/NC/S不同,不理解的可以往上查看。读到这个章节的时候,突然意识到tableB 4.1a/b的含义,其实就是对于轴向受力构件如何通过b/t值来定义with slender 和without slender,而对于弯曲构件,则通过b/t来区别定义Compact/Non-Compact/Slender。
F2:适用于双轴对称的工字型截面和槽钢(翼缘和腹板均为C)
F2开篇重新明确了哪些型钢截面属于这个类别(user notes内容),同时built-up elements我们可以通过table4.1.b来判断。

本小节首先定义了名义屈服强度Mn,其取为塑性屈服极限和LTB屈服极限的较小值,因为F2这类截面的limit state只有Y和LTB,是最简单的抗弯强度设计工况。
这个章节有三个临界侧向无支撑长度可以展开理解一下,LTB这个极限状态下的名义弯矩就是通过构件的实际长度Lb与Lr和Lp的关系来分类计算。不同的无支撑长度会导致F2类截面的LTB强度由不同阶段控制,具体的公式及细节请大家在使用的时候翻看细节使用(公式F2-2、F2-3),这里不做展开描述。
Lb | length between points that are either braced against lateral displacement of the compression flange or braced against twist of the cross section其实就是构件的实际侧向无支撑长度 |
Lp | the limiting laterally unbraced length for the limit state of yielding屈服极限状态下的临界侧向无支撑长度 |
Lr | the limiting unbraced length for the limit state of inelastic lateral-torsional buckling非弹性侧向扭转屈曲极限状态下的临界侧向无支撑长度 |
F3:适用于绕强轴弯曲双轴对称工字型截面(腹板C,翼缘C or NC)
这个小节的截面与F2的工字型截面相比的构件截面区别是翼缘是NC和S的状态,user note也明确了符合要求的F3型钢截面是以下这些:

而它的名义强度由LTB和FLB极限状态控制,即F3截面的Mn取min{LTB,FLB},其中LTB极限状态下的Mn同F2的相关条文。本节主要内容就是明确了FLB极限状态下如何计算弯曲极限强度(公式F3-1即F3-2)。
这一小节遇到了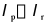 的实际应用,我觉得也是一个很好的定位来理解这两个系数:
的实际应用,我觉得也是一个很好的定位来理解这两个系数:
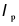
| the limiting width-to-thickness ratio for a compact flange as defined in Table B4.1b 翼缘达到compact的最大宽厚比(翼缘可以充分利用材料屈服强度,即翼缘局部屈服临界应力≥构件屈服强度) |
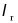
| the limiting width-to-thickness ratio for a non-compact flange as defined in Table B4.1b翼缘达到non-compact的最大宽厚比(翼缘达不到全截面屈服,即翼缘局部屈服临界应力<构件屈服强度) |
其实C/NC/S的定义也是和这两个系数相关,
Compact | b/t≤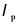 |
Non-compact | 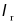 ≥b/t> ≥b/t>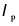
|
Slender | b/t>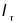 |
F4:绕强轴弯曲的其他工字型截面(腹板C or NC)
这个小节的截面就比较复杂了,腹板和翼缘的宽厚比不再收到限制,就会组合出四个极限状态:CFY、LTB、FLB、TFY。本节的user note提出也可以使用F5计算条文计算F4的截面,F5的计算结果更为保守(这两节的区别就是F5的腹板类型是S,更不利与F4)。而它的名义强度由上述四种极限状态控制,即F4截面的Mn取min{CFY,LTB,FLB,TFY}。
其中CFY极限状态详见公式F4-1;其中LTB极限状态详见公式F4-2及F4-3;其中FLB极限状态详见公式F4-13及F4-14;其中TFY极限状态详见公式F4-15~F4-17。
这一小节也有四个系数,我觉得可以拎出来明确一下他们的含义,在这几个章节里都有大量出现,这四个系数主要也就是用于C和NC截面构件的抗弯强度计算,用来考虑腹板的塑性发展和翼缘的弹性性能的相互作用。
Sxc | elastic section modulus referred to compression flange受压翼缘的弹性截面模量 |
Sxt | elastic section modulus referred to tension flange受拉翼缘的弹性截面模量 |
Rpc | web plastification factor corresponding to the compression flange yielding limit state受压翼缘侧腹板的塑性化系数 |
Rpt | web plastification factor corresponding to the tension flange yielding limit state受拉翼缘侧腹板的塑性化系数 |
F5:绕强轴弯曲的双轴对称和单轴对称工字型截面(翼缘S)
F5相较于F2~F4是截面最严格的一种,它的腹板类型是S,适用于那些腹板相对特别薄的构件截面,这也意味着腹板的局部稳定性最差,无法有效参与塑性变形。F5截面的Mn取min{CFY,LTB,FLB,TFY}。其中CFY极限状态详见公式F5-1;其中LTB极限状态详见公式F5-2;其中FLB极限状态详见公式F5-7;其中TFY极限状态详见公式F5-10。
这一小节见到了一个新的系数Rpg:the bending strength reduction factor,这个值和F4中的Rpc和Rpt其实存在一定的相关性,对于C和NC截面,腹板可以全部或者部分产生塑性变形,而S截面,过于细长的腹板已经无法产生塑性变形,所以通过Rpg系数对整体弯曲强度进行折减,保证S型截面构件的设计安全性。
ØF6: 绕弱轴弯曲的工字型截面和槽钢
F6节用来明确绕弱轴弯曲的截面设计规则,弱轴的惯性矩远小于强轴,弯曲时稳定性相较于强轴更好,其破坏模式由翼缘局部屈曲控制,在实际应用中大多适用于次要构件。它的Mn取min{Y,FLB}。其中Y极限状态详见公式F6-1;其中FLB极限状态详见公式F6-2及F6-3;
其中user note有一个简化计算的提醒,当时下图这些截面是,构件是C型截面,构件的弯曲不会由翼缘局部屈曲控制。

ØF7: 方形和矩形HSS及箱形截面
F7节用来明确方形、矩形和箱型截面,它们的截面特性就让其可以绕任意轴弯曲,适用于多方向受力的情况,所以它的破坏模式也非常“全面”,它的Mn取min{Y,FLB,WLB,LTB}。其中Y极限状态详见公式F7-1;其中FLB极限状态详见公式F7-2及F7-3;其中WLB极限状态详见公式F7-7;其中LTB极限状态详见公式F7-10及F7-11;本节在WLB部分有一条user note,意思简单来说就是在设计的时候要避免设计出web也薄flange也薄的构件,避免双S的产生,本规范无法对双S的box section进行设计。

ØF8: 圆形HSS
这一节讲的round HSS是D/t<0.45E/Fy的截面,它的Mn取min{Y,LB}。其中Y极限状态详见公式F8-1;其中LB极限状态详见公式F8-2及F8-3。
ØF9-F12: 各种角钢双角钢截面
F9:对称平面内受力的T型截面和双角钢
这一节限制了荷载load in the plane of symmetry,其实就是为了保证tees和double angles的受力情况相对简单和明确,构件主要发生弯曲变和局部屈曲破坏,F9的Mn取min{Y,LTB、FLB、LB}。其中Y极限状态详见公式F9-1;其中LTB极限状态详见公式F9-6及F9-7。其中FLB极限状态详见公式F9-14及F9-15;其中LB极限状态详见公式F9-16及F9-17。
F10:单角钢
单角钢比较复杂,拆开来从坐标系角度,角钢可以分为几何轴geometric axis(x,y)和主轴principal axis(u,v)。几何轴是几何截面定义的,而主轴则是由角钢的实际受力决定的。这时候在设计的时候,就有两种情况,情况1:with continuous lateral-torsional restraint有连续侧向扭转约束,使用几何轴进行设计,约束能很好地方式LTB,能简化计算,情况2:without continuous lateral-torsional restraint无连续侧向扭转约束,优先使用主轴进行设计。同时也提醒复杂情况应结合H2的内容一起设计。F10的Mn取min{Y,LTB、leg_LB}。User note也提醒,如果绕着弱轴弯曲,极限状态进需要考虑Y和leg_LB,不需要考虑侧向扭转屈曲。

其中Y极限状态详见公式F10-1;其中LTB极限状态详见公式F10-2及F10-3。其中leg_LB极限状态详见公式F10-6及F10-7。
F11:矩形和圆形杆件
本节的适用范围是Rectangular Bars and Rounds,即绕几何轴弯曲的矩形实心杆和圆形实心杆。它的Mn取min{Y,LTB},其中Y极限状态详见公式F11-1;其中LTB极限状态详见公式F11-3及F11-4。
F12:不对称截面
这一节针对的除了单角钢以外的不对称截面。它的Mn取min{Y,LTB,LB},其中Y极限状态详见公式F12-2;其中LTB极限状态详见公式F12-3;其中LB极限状态详见公式F12-4。这一章节user note也提到,觉得过于保守,是非对称截面的通用设计方法,但是同时也建议设计人员能考虑到经济性,参考附录1.3作为替代进行深化。

ØF13: 受弯构件的局部稳定构造要求
PROPORTIONS OF BEAMS AND GIRDERS,这个标题到底怎么翻译,我觉得很难,最后我取了这个名字,因为我觉得它这一节主要还是讲了受弯构件很多细小的保持局部稳定的构造要求。
1)Strength Reductions for Members with Bolt Holes in the Tension Flange受拉翼缘螺栓孔的强度折减
本段的适用对象轧制或组合截面梁、有盖板的梁、标准或加大螺栓孔、短槽孔或长槽孔(平行于荷载方向)。要求这些构件,在满足F章前面的极限状态以外,Mn还要考虑受拉翼缘的拉伸破坏极限状态tensile rupture of the tension flange。其实就是因为螺栓孔削弱了受拉翼缘的gross section,可能会导致拉伸破坏先于受弯屈服,所以要降低它的抗弯强度。

2)Proportioning Limits for I-Shaped Members H型截面的截面尺寸限制
这一段对单对称H型截面提出了限制性的惯性矩比值要求,是为了控制截面的不对称性,避免过于偏心;对腹板S型H型截面提出了加劲肋的间距限制,其实就是对高厚比提出限制要求,避免产生局部屈曲,使截面无法发挥出充分的设计强度。具体请看原文,不做过多展开。
3)Cover Plates 钢板的连接及构造要求
这一段我感觉讲的members with cover plates通过焊接或螺栓连接钢板来增强构件的抗弯能力,并确保这些钢板能够有效参与抗弯。也提到了螺栓连接和焊接连接时需要按弯曲产生的剪力进行复核,确保使盖板与原构件协同工作。同时构造间距要求、焊缝要求等也做了明确。其实核心就是确保合理的连接能确保荷载的传递。

4)Built-Up Beams 组合构件
这一段的主要核心内容就是要确保结构的整体性、保证荷载的有效传递同时提高整体的刚度。

本期内容主要就是CHAPTER F,屈曲这个章节内容实在是太多了,有遗漏或者错漏的大家可以留言,或者加入交流群一起探索。
