前馈控制的学习笔记,简单理解

PID控制器依赖偏差来得到控制量，为了加快系统达到稳定，可以加入前馈环节

设要控制的系统传递函数为1/(3s+1)，一个简单的前馈如下图，就是先向系统加上指令值乘以一个系数，在下图闭环系统中，系数为1就是先向该系统输入1，相当于在调节初期提高了控制量，考虑到系统为开环时向该系统输入1，则在稳态后输出1，加入这个前馈只会让稳态时从PID模块出来的值为0，不会产生稳态误差。

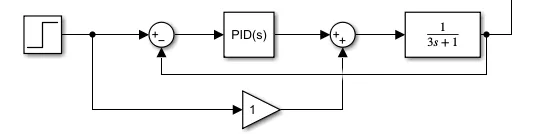
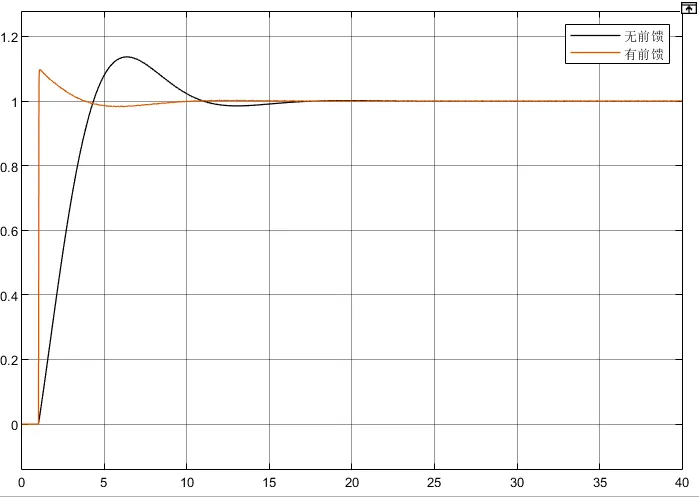
在相同的PI控制器下对比有无前馈时的响应如下，可以看到由于前馈在初期加入了一个值，超调会大

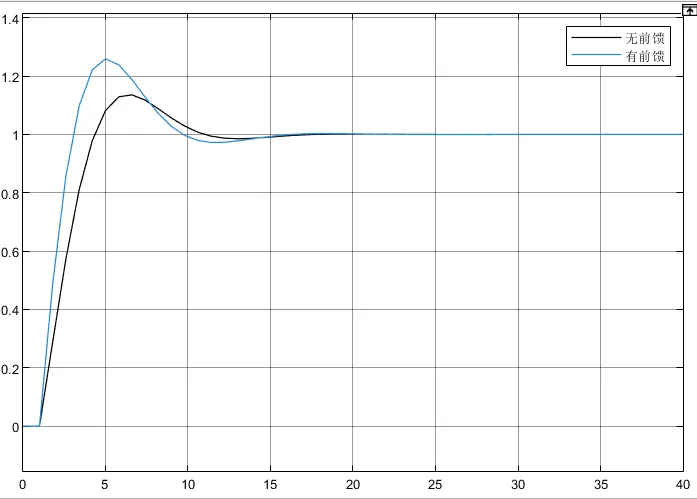
可以优化该“系数”项，根据参考[2]，先看误差传递函数，令分子项为0，得到对于惯性环节G=k/(Ts+1)，前馈函数的“系数”项为传递函数(Ts+1)/k，恰好为系统传递函数的倒数，这并不是偶然，因为误差为0即系统的输出Y等于指令信号R，考虑到输入系统的控制量U与Y间满足Y=GU，因此若要输出R，则输入U应等于G^(-1)R。对于这个案例，前馈如下图

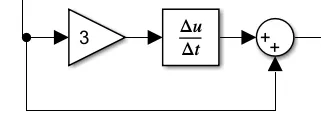
不过似乎没有体现出前馈的优势

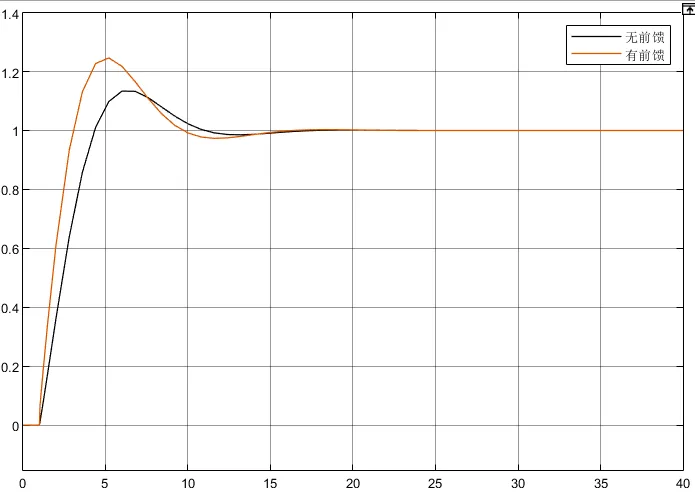
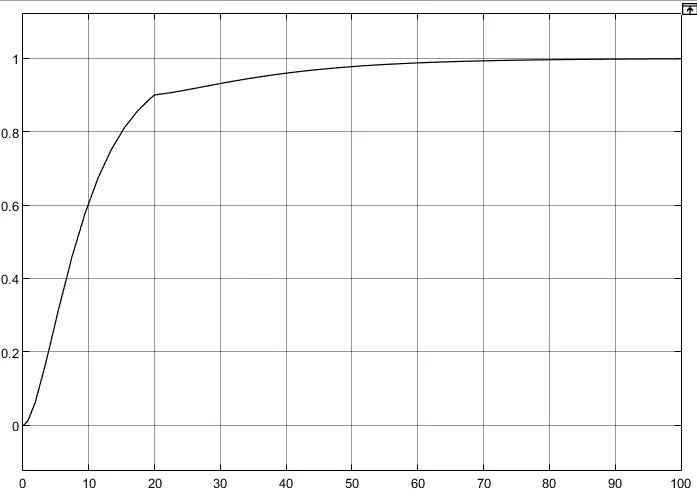
这是因为涉及微分环节，而阶跃信号的微分为无穷大，在阶跃信号后接一个时间常数很小（0.01）的惯性环节作为滤波器，再次仿真，可以看到输出信号立刻上去，且调节时间也很短。

以上是对参考信号的前馈，前馈也可以针对干扰信号，这在涡轴发动机中很常用

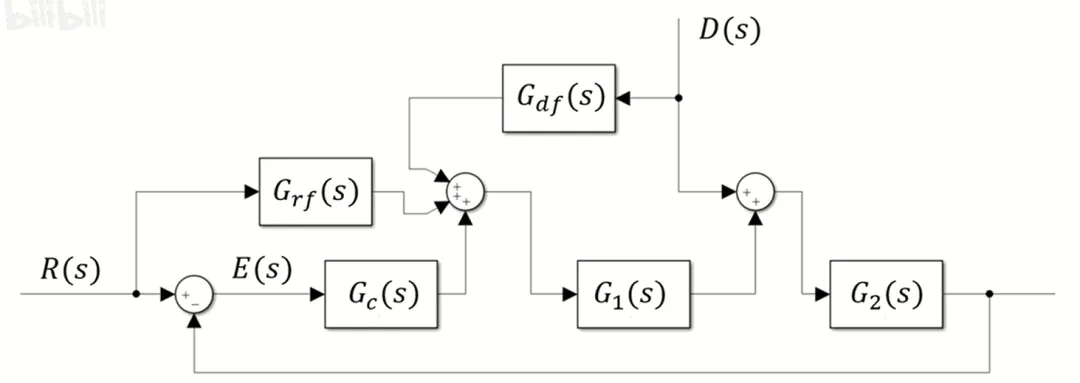
根据[2]，两个前馈表达式为

设G1和G2都是1/(3s+1)，则Grf(s)要求两次微分，这在实际中会很慢。

参考[1]给出如下的，Gd为前馈传递函数，显然Gd=-Gf/G2时可以抵消干扰

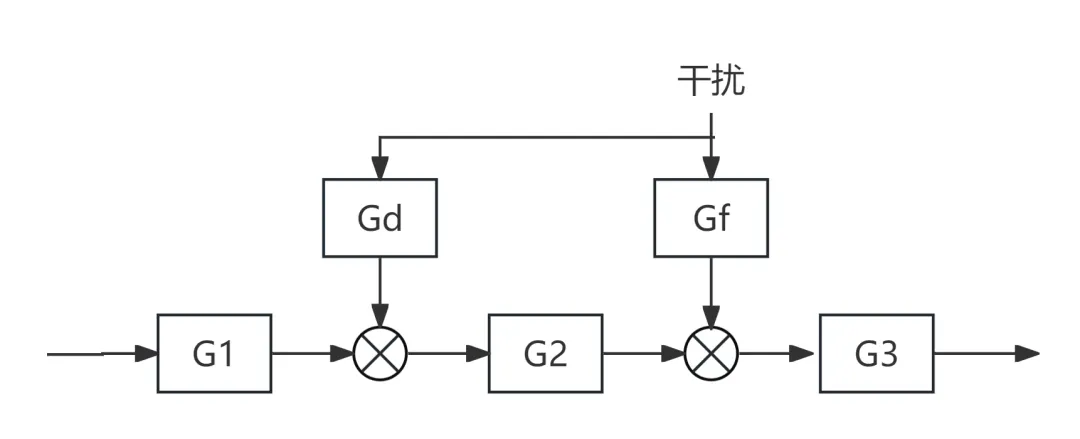
参考例9-6给出各个传递函数，模型如下

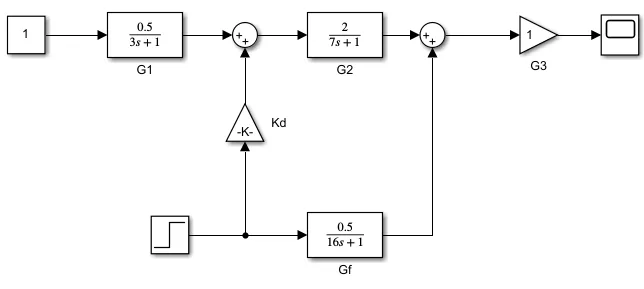
不过现实情况是没有这么明确的传递函数，且考虑到对于高阶系统的前馈传递函数难以避免微分项，因此[1]将Gd项简化为常数，还在214页给出了工程整定的方法，就是逐渐调整Kd使系统的输出回到指令值。书里给出此时Kd=-0.25，此时响应如下图，当然由于只有前馈，此时系统的响应还是很慢。

参考

1. 王正林,郭阳宽.MATLAB/Simulink与过程控制系统仿真[M].北京:电子工业出版社,2012.例9-6

2. 只用PID?加上前馈解决95%的问题！_哔哩哔哩_bilibili