3 动量守恒定律
[学习目标] 1.了解系统、内力、外力的概念。2.会根据动量定理、牛顿第三定律推导动量守恒定律，理解动量守恒定律从“动量”的角度描述物体间的相互作用的本质(重点)。3.能在具体问题中判断动量是否守恒，能熟练运用动量守恒定律解释相关现象和解决相关问题(重难点)。
一、相互作用的两个物体的动量改变
如图所示，在光滑水平桌面上沿同一方向做匀速运动的两个物体，质量为m2的B物体追上质量为m1的A物体，并发生碰撞，设A、B两物体碰前速度分别为v1、v2(v2>v1)，碰后速度分别为v1′、v2′，碰撞时间很短，设为Δt。设B对A的作用力是F1，A对B的作用力是F2。
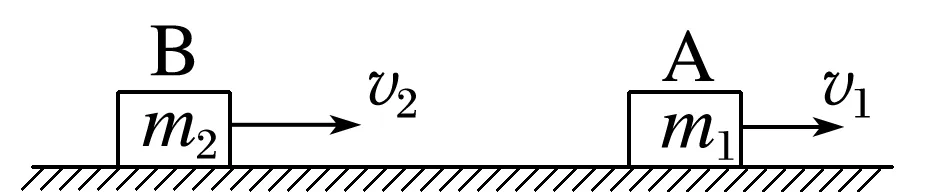
请用所学知识证明碰撞前后两物体总动量之和相等。
答案 根据动量定理：
对A：F1Δt＝m1v1′－m1v1①
对B：F2Δt＝m2v2′－m2v2②
由牛顿第三定律得F1＝－F2③
由①②③得两物体总动量关系为：
m1v1′＋m2v2′＝m1v1＋m2v2。
二、动量守恒定律
1．系统、内力与外力
(1)系统：两个(或多个)相互作用的物体构成的整体叫作一个力学系统。
(2)内力：系统中物体间的作用力。
(3)外力：系统以外的物体施加给系统内物体的力。
2．动量守恒定律
(1)内容：如果一个系统不受外力，或者所受外力的矢量和为0，这个系统的总动量保持不变。
(2)表达式：
m1v1＋m2v2＝m1v1′＋m2v2′(作用前后总动量相等)，即p＝p′。
说明：动量守恒定律其他表现形式
①Δp＝0，表示系统总动量的增量等于零。
②Δp1＝－Δp2，其中Δp1、Δp2分别表示系统内两个物体动量的变化量，即两个物体组成的系统，两物体动量的增量大小相等、方向相反。
(3)适用条件：系统不受外力或者所受外力的矢量和为零。
(4)普适性：动量守恒定律既适用于低速物体，也适用于高速(接近光速)物体。既适用于宏观领域，也适用于微观领域。
如图所示，光滑的水平面上两小车中间夹一压缩的轻弹簧，两手分别按住小车使它们静止，对两车及弹簧组成的系统，试分析：
(1)两手同时放开，两车的动量均不为0，它们的总动量是否增加了？
(2)若先放开左手，再放开右手后，系统的总动量是否为0？若不为零，方向如何？之后系统的总动量是否守恒？
答案 (1)虽然两小车的动量都不为0，但由于动量是矢量，根据动量守恒定律，它们的总动量仍然为0，并没有增加。
(2)先放开左手，左边的小车就向左运动，当再放开右手后，系统总动量不为0，方向向左。之后系统所受合外力为零，系统总动量守恒。
(多选)如图所示的过程中，系统的动量守恒的有( )
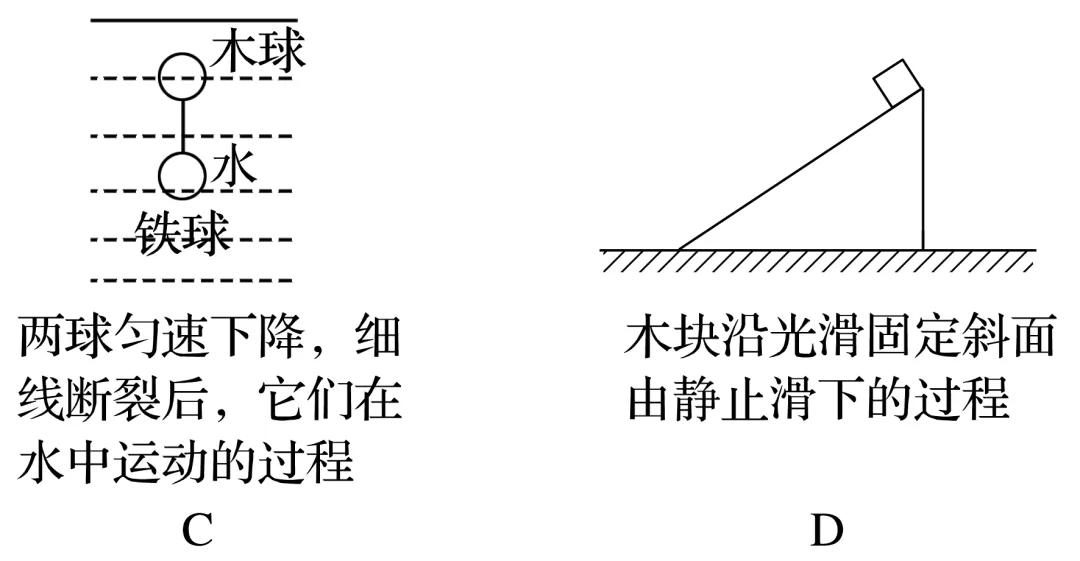
答案 AC
解析 选项A中，子弹射入木块的过程中，系统所受合外力为零，则动量守恒；选项B中，剪断细线，压缩的轻弹簧恢复原长的过程中，水平方向要受到竖直墙壁对M的作用力，即水平方向所受合外力不为零，系统的动量不守恒；选项C中，两球匀速下降，则受到的重力和浮力的合力为零，细线断裂后，系统所受的重力和浮力不变，则系统所受合外力仍为零，系统动量守恒；选项D中，木块沿光滑固定斜面下滑的过程中，系统所受合外力不为零，系统动量不守恒，故A、C正确。
针对训练 2022年北京冬奥会，中国选手顺利拿下花样滑冰双人滑自由滑总分第一名，为中国代表团拿到北京冬奥会第九枚金牌。比赛中，两个人静立在赛场中央，互推后各自沿直线后退，然后进行各种表演。女选手的质量小于男选手的质量，假设双人滑冰场地为光滑冰面，下列关于两个人互推前后的说法正确的是( )
A．静止在光滑的冰面上互推后瞬间，两人的总动量不再为0
B．静止在光滑的冰面上互推后瞬间，两人的总动量为0
C．男选手质量较大，互推后两人分离时他获得的速度较大
D．女选手质量较小，互推后两人分离时她获得的速度较小
答案 B
解析 静止在光滑的冰面上互推后瞬间，合外力为0，动量守恒，两人的总动量为0，故A错误，B正确；根据动量守恒m1v1＝m2v2，男选手质量较大，获得的速度较小，女选手质量较小，获得的速度较大，故C、D错误。
系统动量是否守恒的判定方法
1．选定研究对象及研究过程，分清外力与内力。
2．分析系统受到的外力矢量和是否为零，若外力矢量和为零，则系统动量守恒；若外力在某一方向上合力为零，则在该方向上系统动量守恒。系统动量严格守恒的情况很少，在分析具体问题时要注意把实际过程理想化。
3．除了利用动量守恒条件判定外，还可以通过实际过程中系统各物体各方向上总动量是否保持不变来进行直观的判定。
三、动量守恒定律的简单计算
质量为3 kg的小球A在光滑水平面上以6 m/s的速度向右运动。
(1)若遇上质量为5 kg、以4 m/s的速度向左运动的小球B，碰撞后B球恰好静止，求碰撞后A球的速度；
(2)若遇上质量为2 kg、静止的小球B，碰撞后A和B一起继续运动，求碰撞后两球共同的速度。
答案 (1)23 m/s，方向向左
(2)3.6 m/s，方向向右
解析 (1)取向右为正方向，根据动量守恒定律
mAvA－mBvB＝mAvA′＋0
解得vA′＝－23 m/s，负号代表方向向左。
(2)取向右为正方向，根据动量守恒定律
mAvA＝(mA＋mB′)v
解得v＝3.6 m/s，方向向右。
光滑水平面上滑块A与滑块B在同一条直线上发生碰撞，它们运动的位移x与时间t的关系图像如图所示，已知滑块A的质量为1 kg，碰撞时间不计，则滑块B的质量为( )
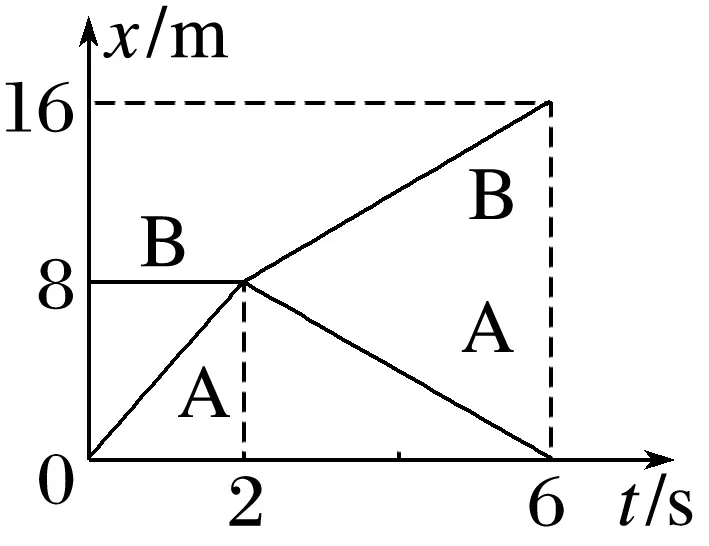
A．1 kgB．2 kgC．3 kgD．4 kg
答案 C
解析 因x－t图像的斜率表示速度，由图像可知，碰前A的速度为vA1＝82 m/s＝4 m/s，碰前B的速度为零，碰后A的速度为vA2＝0－84 m/s＝－2 m/s，碰后B的速度为vB2＝16－84 m/s＝2 m/s，根据动量守恒定律mAvA1＝mAvA2＋mBvB2，解得mB＝3 kg，故选C。
一枚在空中飞行的火箭质量为m，在某时刻的速度大小为v，方向水平，燃料即将耗尽。此时，火箭突然炸裂成两块，其中质量为m1的一块沿着与v相反的方向飞去，速度大小为v1。求炸裂后另一块的速度v2。
答案 mv＋m1v1m－m1，方向与炸裂前火箭速度方向相同
解析 以炸裂前火箭速度方向为正方向，
炸裂前火箭的总动量为：p＝mv
炸裂后火箭的总动量为：p′＝－m1v1＋(m－m1)v2
根据动量守恒定律有：mv＝－m1v1＋(m－m1)v2
可得：v2＝mv＋m1v1m－m1
炸裂后此块与炸裂前火箭速度方向相同。
应用动量守恒定律解题的思路
明确研究对象，确定系统的组成
↓
受力分析，分清内力、外力，确定动量是否守恒
↓
规定正方向，确定初、末动量
↓
根据动量守恒定律，建立方程
↓
代入数据，求出结果并讨论说明
课时对点练
通过网盘分享的文件：【淘宝店：品优教学】赠送等3个文件
链接: https://pan.baidu.com/s/1W_-FY-AxO_3dspNZY2P-vQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享
