网架结构作为应用最为广泛的空间网格结构，尽管造型复杂多变，但最基础的静力计算程序核心代码仅需千余行，其计算理论简洁经典，可以说是空间结构设计必备的理论知识。本文对网架结构的静力计算理论进行梳理与总结。在这一步骤中，建立网架结构的线模型，并赋予杆件截面、材料荷载及约束等结构信息。在这一步骤中，先在单元坐标系中形成单元刚度矩阵，然后转换成整体坐标系中的刚度矩阵。单元坐标系中，在小变形时，节点1，2的节点力与节点位移的关系可表示为为便于将单元刚度矩阵组装到整体刚度矩阵中，需要将公式（2）、（3）转换成整体坐标系oxyz中。记杆件在整体坐标系中的单位方向向量为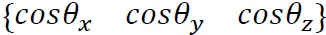
，简记为
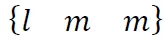，坐标转换矩阵T为则整体坐标系下的节点位移与单元坐标系下的节点位移的关系式为:同理整体坐标系下的节点荷载与单元坐标系下的节点荷载的关系式为:将式（6）（8）代入式（3）,两边同乘坐标转换矩阵T的转置网架结构由成千上万个单元组成，每个单元都有相应的单元刚度矩阵，将整体坐标系下的单元刚度矩阵按照“对号入座”的方式“送入”总体刚度矩阵相应位置，即可得到整个结构的总体刚度矩阵K。设节点i,j之间有杆单元，其相应的单元刚度矩阵为
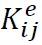，矩阵中的各数值用黄色表示;节点j,k之间有杆单元，其相应的单元刚度矩阵为
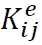，矩阵中的各数值用绿色表示。按下图所示，根据矩阵中的数值代表哪两个自由度的关系，“送入”总体刚度矩阵相应位置，在同一位置有多个元素式，将多个元素相加，即可得到总体刚度矩阵。如果结构的总自由度数量为nf，则总体刚度矩阵的维数为nf×nf。按照以上方法组装的总体刚度矩阵是奇异的，即方程K∙U=0，U有非零解，其物理意义为结构仅平移时，节点力向量为零。实际结构由于有约束，结构的总体刚度矩阵非奇异。为反映约束对结构总体刚度矩阵的影响，程序设计时常采用“充大数”法修正刚度矩阵。在式（12）的刚度矩阵中，如节点i的x向位移被约束，可认为此自由度对应的刚度为无穷大，将ix行ix列位置的元素数值改成一个大数，如1e10，即代表刚度无限大，相当于被约束，这种做法的好处是结构刚度矩阵规整，利于编程。网架结构受约束的自由度对应的节点外荷载（即支座反力）未知，但位移已知（本文仅讨论刚性支座），即为零；未受约束自由度对应的外荷载已知，但位移未知。这样对于有nf个自由度的结构，总共有nf个未知数，nf个方程，解线性方程组可求出唯一解。第5步求得的nf个未知数的解，一部分为受约束自由度对应的支座反力，一部分为未受约束的自由度对应的节点位移。求得杆件整体坐标系中杆件节点位移后，杆件轴力按下式计算，拉力为正，压力为负。本文介绍了网架结构的静力计算理论，包括单元刚度矩阵的计算、总体刚度矩阵的组装、根据边界条件修正总体刚度矩阵的方法、以及杆件位移、内力及支座反力的计算方法。DS公众号，敬请关注
www.directsolution.com.cn
DS真诚希望成为您的专业伴侣，
一起在专业的路上携手并进！
10个月宝宝每天需要喝多少奶粉？
